1. 卷积神经网络的基础概念
卷积神经网络是一种专门用来处理具有类似网络结果的数据的神经网络。至少在网络的一层中使用卷积运算来替代一般的矩阵乘法运算的神经网络。
最核心的几个思想:稀疏交互、参数共享、等变表示(通俗成为平移不变性)。根本目的说白了就是为了节省运算时间和空间。那接下来看一下是怎么实现的。
1.0 卷积
用一张图展示一下,卷积的计算。element-wise multiply 然后再相加。
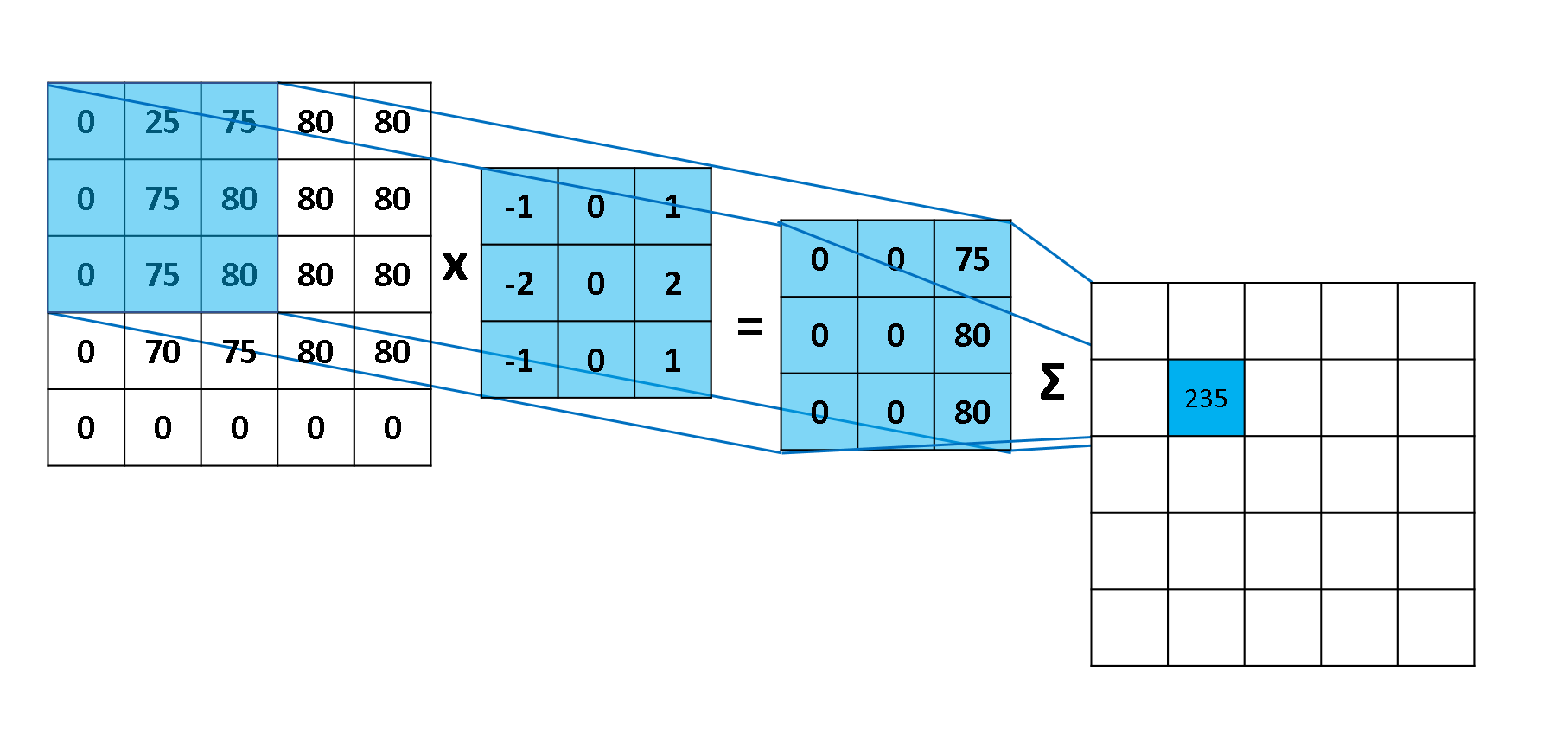
看一下动图,感受一下整个滑动计算的过程。
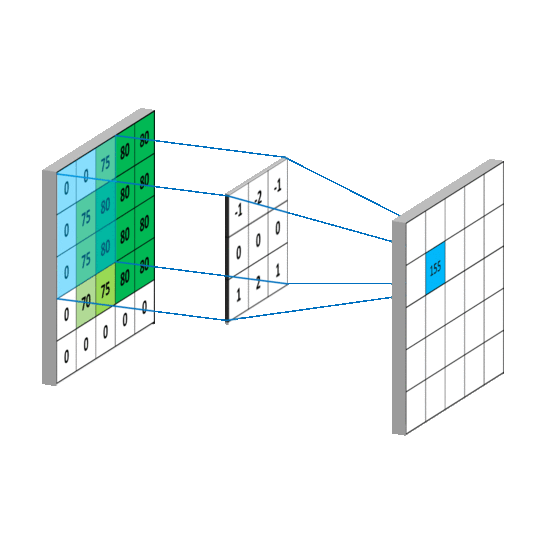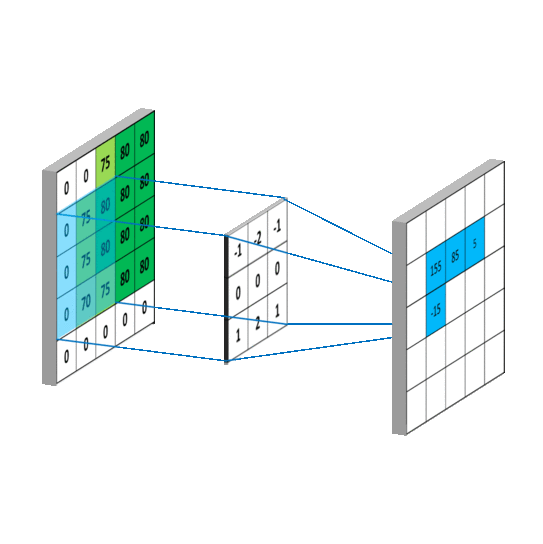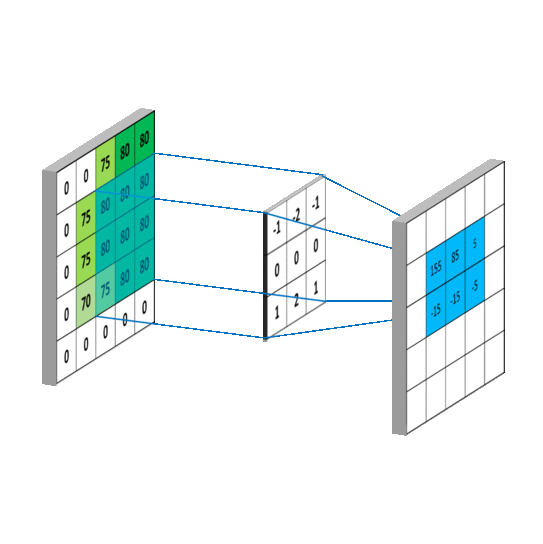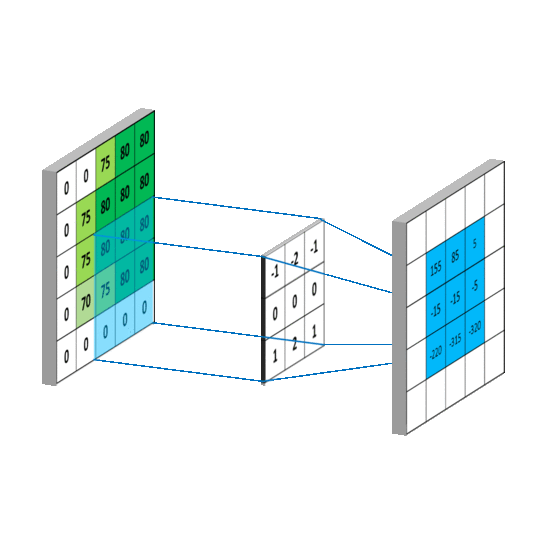
1.1 稀疏交互(连接数下降到k)
传统的神经网络使用矩阵乘法来建立输入与输出的连接关系。参数矩阵中每一个单独的参数都描述了一个输入单元与一个输出的单元间的交互。这意味着每一个输出单元与每一个输入单元都产生交互(例如全连接层)。而卷积网络限制连接数,使其具有稀疏交互或者稀疏权重的特征,使核的大小远小于输入的大小来达到。
例如原先有m个输入和n个输出,如果矩阵乘法需要 m*n 个参数,时间复杂度为 O(m*n)。卷积是限制每一个输出拥有的连接数为 k,那么稀疏的连接方法只需要 k*n 个参数,以及运行时间为 O(k*n)。实际操作中,k比m小几个数量级,而且在机器学习中能取得较好的表现,因而十分有效。
1.2 参数共享(使用同一个连接,下降到了1)
参数共享的定义是指在一个模型的多个函数中使用相同的参数。用于一个输入的权重也会被绑定在其他的权重上。在卷积神经网络中,核的每个元素都作用在每一个位置上。卷积运算中的参数共享保证了我们只需要学习一个参数集合,并不需要对每个位置都学习单独的参数集合。它的前向传播时间仍旧为 O(k*n), 但只需要存储k个参数。大大降低了存储量。
这个问题容易出现在面试问答中,需要理解其中的原理与动机。
1.3 平移等变
如果一个函数满足输入改变,输出也以同样的方式改变,它就是等变的。这个特征可以说是有利有弊吧。先看有利的地方。举个例子,令 I 为图像的亮度函数,g 为图像函数的变换函数(把一个图像函数映射到另一个图像函数的函数)使得 I' = g(I), 这里可以假设 g 是使 I 中每个像素右移一位。同样,如果先对图像进行右移,再进行卷积操作,和先进行卷积操作,再进行右移,所得到的结果是一样的。
具体证明,可以使用傅里叶变换(可以参考知乎这篇回答 https://zhuanlan.zhihu.com/p/44769370 ),这里主要讲一下直观的理解,例如某一卷积核为了检测边缘,在图像中,各种位置均会有相似边缘,而权值共享使得在各位置出现的边缘均能被激活。总体来看,该特征与位置无关,对位置不敏感。这对于分类来说,十分有效,但对于与位置相关的任务来说,就不那么合适了,比如目标检测、语义分割等任务,我们不仅需要类别特征,更需要位置信息,平移不变性这个特性是我们不想要的,因而会采取一定的措施,弥补位置信息。
2. 关键细节的计算
在卷积中,有几个关键参数:feature map, kernel_size, stride, padding。
2.1 feature map 和 kernel_size
这两个参数很简单,就是特征图的尺寸和卷积核的尺寸。需要注意的就是表示形式,一般我们常用的矩阵为 c*h*w,c是channel, 即通道数,如果RGB 为 3通道 c=3,黑白图像 c=1。在实际训练中,batch size 往往不为1, 因此 feature map 更常见的情况是四维,b*c*h*w。另外可能出现的问题是,输入的形式为 b*h*w*c。 即要把channel放到最后一个维度。这就要求我们在前期做好数据预处理的工作。kernel_size也是类似,但是只需要 h*w 两维,具体数目取决于输入尺寸与相应输出尺寸。
2.2 stride
stride是步长(步幅)。我们在卷积过程中,有时会希望跳过核中的一些位置来降低计算的开销,当然同时,提取的特征就没有之前那么好。这一过程,也叫做下采样,在输出的每个方向上每间隔 s 个像素进行采样。可以看下图,就是以步长为2在做卷积。

2.3 padding
卷积有一个重要的性质,隐含地对输入V用0进行填充 (pad),使它加宽。因为在卷积的过程中,宽度在每一层会缩减,对输入进行0填充,能帮助我们对输出大小进行有效控制。padding主要有三种方式:第一种是最简单的 VALID, 就是不填充。第二种是SAME,进行足够的零填充保持输入和输出匹配(注意:匹配不代表相同,只是要求输出结果跟指定的输出结果相同大小,如果没有指出输出大小,要求输入输出相同)。最后一种是 FULL,它保证足够多的零填充,使得每个像素在每个方向上刚好被访问 k 次。更加直观来说,添加padding为k-1,即从第一个像素开始能被访问k次。同样看下示意图:

图2.31 VALID 方式
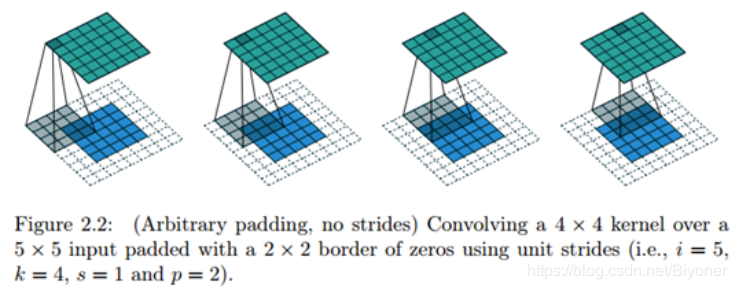
图2.32 SAME 方式(添加一定数量的padding,使输入输出尺寸匹配,具体添加大小根据计算确定)
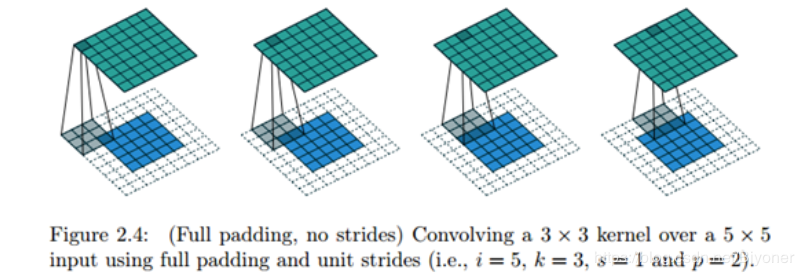
图2.33 FULL 方式
卷积会带来的两个问题:1,卷积运算后,输出图像的尺寸会缩小; 2 越是边缘的像素点,对输出的影响就越小,卷积的时候移到边缘就结束了,但是中间的像素点有可能会参与多次计算,但是边缘的像素点可能只参与一次计算,因此可能会丢失边缘信息。
padding的用途: 保持边界信息;可以对有差异的图片进行补齐,使得图像的输入大小一致;在卷积层中加入padding ,会使卷基层的输入维度与输出维度一致; 同时,可以保持边界信息。
2.4 尺寸计算公式
![]()
![]() : 输入图像的尺寸,例如输入图像的高 h 或 宽 w;
: 输入图像的尺寸,例如输入图像的高 h 或 宽 w;
![]() : 输出图像的尺寸,对应输入的高或宽;
: 输出图像的尺寸,对应输入的高或宽;
![]() :卷积核尺寸
:卷积核尺寸
![]() : 补零
: 补零
![]() :步长
:步长
因而,根据上述公式,可以计算出不同补零方式的值:
VALID: pad = 0; output = (input-kernel)/stride + 1 SAME: input = output; pad=[(output-1)*stride+kernel-input]/2 FULL: pad = kernel-1; output = (input+kernel-2)/stride + 1
3. 代码实现
3.1 基于tensorflow的实现
首先,tensorflow中 二维卷积的实现:
tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, name=None)
input:指需要做卷积的输入图像,它要求是一个Tensor,具有[batch, in_height, in_width, in_channels]这样的shape,具体含义是[训练时一个batch的图片数量, 图片高度, 图片宽度, 图像通道数],注意这是一个4维的Tensor,要求类型为float32和float64其中之一
第二个参数filter:相当于CNN中的卷积核,它要求是一个Tensor,具有[filter_height, filter_width, in_channels, out_channels]这样的shape,具体含义是[卷积核的高度,卷积核的宽度,图像通道数,卷积核个数],要求类型与参数input相同,有一个地方需要注意,第三维in_channels,就是参数input的第四维
第三个参数strides:卷积时在图像每一维的步长,这是一个一维的向量,长度4
第四个参数padding:string类型的量,只能是"SAME","VALID"其中之一,这个值决定了不同的卷积方式(后面会介绍)
实现:(为了简化运算,使用了batch_size =1)
class Conv(object):
def __init__(self,input_data,weights_data,stride,padding='SAME'):
const_input = tf.constant(input_data, tf.float32)
const_weight = tf.constant(weights_data, tf.float32)
input = tf.Variable(const_input, name="input")
input = self.chw2hwc(input)
self.input = tf.expand_dims(input, 0)
weights = tf.Variable(const_weight, name="weights")
weights = self.chw2hwc(weights)
self.weights = tf.expand_dims(weights, 3)
self.stride = stride
self.padding = padding
def get_shape(self,tensor):
[s1,s2,s3] = tensor.get_shape()
s1 = int(s1)
s2 = int(s2)
s3 = int(s3)
return s1,s2,s3
def chw2hwc(self,chw_tensor):
chw_tensor = tf.transpose(chw_tensor,[1,2,0])
return chw_tensor
def hwc2chw(self,hwc_tensor):
hwc_tensor = tf.transpose(hwc_tensor,[2,0,1])
return hwc_tensor
def tf_conv2d(self):
"""
tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, name=None)
"""
conv = tf.nn.conv2d(self.input, self.weights, strides=self.stride, padding=self.padding)
rs = self.hwc2chw(conv[0])
return rs
class CompatV1Conv(object):
def __init__(self,input_data,weights_data,stride,padding='SAME'):
const_input = tf.constant(input_data, tf.float32)
const_weight = tf.constant(weights_data, tf.float32)
input = tf.Variable(const_input, name="input")
input = self.chw2hwc(input)
self.input = tf.expand_dims(input, 0)
weights = tf.Variable(const_weight, name="weights")
weights = self.chw2hwc(weights)
self.weights = tf.expand_dims(weights, 3)
self.stride = stride
self.padding = padding
def get_shape(self,tensor):
[s1,s2,s3] = tensor.get_shape()
s1 = int(s1)
s2 = int(s2)
s3 = int(s3)
return s1,s2,s3
def chw2hwc(self,chw_tensor):
chw_tensor = tf.transpose(chw_tensor,[1,2,0])
return chw_tensor
def hwc2chw(self,hwc_tensor):
hwc_tensor = tf.transpose(hwc_tensor,[2,0,1])
return hwc_tensor
def tf_conv2d(self):
"""
tf.compat.v1.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, name=None)
"""
conv = tf.compat.v1.nn.conv2d(self.input, self.weights, strides=self.stride, padding=self.padding)
rs = self.hwc2chw(conv[0])
return rs
代码主要包括以下几个部分:
1)对于数据格式进行预处理,使 c*h*w 的数据变为 h*w*c
2)调用 tf.nn.conv2d
3)将结果转换成常用 c*h*w 的格式
调用:
import tensorflow as tf # c*h*w shape=[c,h,w] input_data = [ [[1, 0, 1, 2, 1], [0, 2, 1, 0, 1], [1, 1, 0, 2, 0], [2, 2, 1, 1, 0], [2, 0, 1, 2, 0]], [[2, 0, 2, 1, 1], [0, 1, 0, 0, 2], [1, 0, 0, 2, 1], [1, 1, 2, 1, 0], [1, 0, 1, 1, 1]], ] # in_c*k*k weights_data = [ [[1, 0, 1], [-1, 1, 0], [0, -1, 0]], [[-1, 0, 1], [0, 0, 1], [1, 1, 1]] ] conv = Conv(input_data,weights_data,stride=[1,1,1,1]) rs = conv.tf_conv2d() init = tf.global_variables_initializer() sess = tf.Session() sess.run(init) conv_val = sess.run(rs) print(conv_val[0])
import tensorflow as tf # c*h*w shape=[c,h,w] input_data = [ [[1, 0, 1, 2, 1], [0, 2, 1, 0, 1], [1, 1, 0, 2, 0], [2, 2, 1, 1, 0], [2, 0, 1, 2, 0]], [[2, 0, 2, 1, 1], [0, 1, 0, 0, 2], [1, 0, 0, 2, 1], [1, 1, 2, 1, 0], [1, 0, 1, 1, 1]], ] # in_c*k*k weights_data = [ [[1, 0, 1], [-1, 1, 0], [0, -1, 0]], [[-1, 0, 1], [0, 0, 1], [1, 1, 1]] ] tf.compat.v1.disable_eager_execution() conv = CompatV1Conv(input_data,weights_data,stride=[1,1,1,1]) rs = conv.tf_conv2d() init = tf.compat.v1.global_variables_initializer() sess = tf.compat.v1.Session() sess.run(init) conv_val = sess.run(rs) print(conv_val[0])
import tensorflow as tf # c*h*w shape=[c,h,w] input_data = [ [[1, 0, 1, 2, 1], [0, 2, 1, 0, 1], [1, 1, 0, 2, 0], [2, 2, 1, 1, 0], [2, 0, 1, 2, 0]], [[2, 0, 2, 1, 1], [0, 1, 0, 0, 2], [1, 0, 0, 2, 1], [1, 1, 2, 1, 0], [1, 0, 1, 1, 1]], ] # in_c*k*k weights_data = [ [[1, 0, 1], [-1, 1, 0], [0, -1, 0]], [[-1, 0, 1], [0, 0, 1], [1, 1, 1]] ] conv = Conv(input_data,weights_data,stride=[1,1,1,1]) rs = conv.tf_conv2d() print(rs)
3.2 基于python 与 numpy 的实现
与上面不同,这里不需要处理数据格式,但需要对参数进行人为约束,主要分为以下几个方面:
class myConv(object):
def __init__(self,input_data,weight_data,stride,padding='SAME'):
self.input = np.asarray(input_data, np.float32)
self.weights = np.asarray(weights_data, np.float32)
self.stride = stride
self.padding = padding
def compute_conv(self,fm,kernel):
[h,w] = fm.shape
[k,_] = kernel.shape
if self.padding == 'SAME':
pad_h = (self.stride *(h-1) + k - h)//2
pad_w = (self.stride *(w-1) + k - w)//2
rs_h = h
rs_w = w
elif self.padding == 'VALID':
pad_h = 0
pad_w = 0
rs_h = (h-k)/self.stride+1
rs_w = (w-k)/self.stride+1
elif self.padding == 'FULL':
pad_h = k-1
pad_w = k-1
rs_h = (h+k-2)/self.stride+1
rs_w = (w+k-2)/self.stride+1
else:
pad_h = 0
pad_w = 0
rs_h = (h - k) / self.stride + 1
rs_w = (w - k) / self.stride + 1
padding_fm = np.zeros([h+2*pad_h,w+2*pad_w],np.float32)
padding_fm[pad_h:pad_h+h,pad_w:pad_w+w] = fm
rs = np.zeros([rs_h,rs_w],np.float32)
for i in range(rs_h):
for j in range(rs_w):
roi = padding_fm[i*self.stride:(i*self.stride+k),j*self.stride:(j*self.stride+k)]
rs[i][j] = np.sum(roi*kernel)
return rs
def my_conv2d(self):
"""
self.input:c*h*w
self.weights:c*h*w
:return:
"""
[c,h,w] = self.input.shape
[kc,k,_] = self.weights.shape
assert c==kc
outputs = []
for i in range(c):
f_map = self.input[i]
kernel = self.weights[i]
rs = self.compute_conv(f_map,kernel)
if outputs==[]:
outputs = rs
else:
outputs += rs
return outputs
1. 首先根据 pad 的形式,对输入进行补零操作;
2. 其次根据 input,pad, stride 利用公式计算输出大小;
3. 然后进行循环进行卷积操作,对不同channel进行卷积,再相加,得到卷积后的结果。具体也可以看上面的动图,整体实现会比较清楚。
调用:
import numpy as np # c*h*w shape=[c,h,w] input_data = [ [[1, 0, 1, 2, 1], [0, 2, 1, 0, 1], [1, 1, 0, 2, 0], [2, 2, 1, 1, 0], [2, 0, 1, 2, 0]], [[2, 0, 2, 1, 1], [0, 1, 0, 0, 2], [1, 0, 0, 2, 1], [1, 1, 2, 1, 0], [1, 0, 1, 1, 1]], ] # in_c*k*k weights_data = [ [[1, 0, 1], [-1, 1, 0], [0, -1, 0]], [[-1, 0, 1], [0, 0, 1], [1, 1, 1]] ] conv = myConv(input_data,weights_data,1,'SAME') print(conv.my_conv2d())
最后,两者输出的结果相同,说明我们的实现是正确的。
具体的输出结果如下:
[[ 2. 0. 2. 4. 0.] [ 1. 4. 4. 3. 5.] [ 4. 3. 5. 9. -1.] [ 3. 4. 6. 2. 1.] [ 5. 3. 5. 1. -2.]]
C++版本代码:
#include <stdlib.h>
#include <memory.h>
#include <stdio.h>
#define DEBUG (0)
typedef struct _T {
int channel;
int width;
int height;
void* data;
}Tensor;
typedef enum {
VALID,
SAME,
FULL
} PADDING;
static Tensor* pad_input(const Tensor& input_data, const Tensor& weights_data, Tensor& out_data, const unsigned int stride, const PADDING padding) {
Tensor* tensor = (Tensor*)malloc(sizeof(Tensor));
int len = sizeof(int) * input_data.channel * input_data.width * input_data.height;
int pad_w = 0;
int pad_h = 0;
int* data = NULL;
//output = (input - kernel + 2* pad) / stride + 1;
if (SAME == padding) {
//input = output; pad = ((output - 1) * stride - input + kernel) / 2
pad_w = ((input_data.width - 1) * stride - input_data.width + weights_data.width) / 2;
pad_h = ((input_data.height - 1) * stride - input_data.height + weights_data.height) / 2;
tensor->width = input_data.width + pad_w * 2;
tensor->height = input_data.height + pad_h * 2;
tensor->channel = input_data.channel;
len = sizeof(int) * input_data.channel * (input_data.width + pad_w * 2) * (input_data.height + pad_h * 2);
data = (int*)malloc(len);
tensor->data = data;
memset(data, 0, len);
int* in_data = (int*)input_data.data;
for(int c = 0; c < input_data.channel; c++){
for(int h = 0; h < input_data.height; h++) {
for(int w = 0; w < input_data.width; w++) {
data[c * tensor->width * tensor->height + tensor->width * (h + pad_h) + w + pad_w] = in_data[c * input_data.width * input_data.height + input_data.width * h + w];
}
}
}
} else if(FULL == padding) {
//pad = kernel-1; output = (input+kernel-2)/stride + 1
pad_w = input_data.width - 1;
pad_h = input_data.height - 1;
tensor->width = input_data.width + pad_w * 2;
tensor->height = input_data.height + pad_h * 2;
tensor->channel = input_data.channel;
len = sizeof(int) * input_data.channel * (input_data.width + pad_w * 2) * (input_data.height + pad_h * 2);
data = (int*)malloc(len);
tensor->data = data;
memset(data, 0, len);
int* in_data = (int*)input_data.data;
for(int c = 0; c < input_data.channel; c++){
for(int h = 0; h < input_data.height; h++) {
for(int w = 0; w < input_data.width; w++) {
data[c * tensor->width * tensor->height + tensor->width * (h + pad_h) + w + pad_w] = in_data[c * input_data.width * input_data.height + input_data.width * h + w];
}
}
}
} else {
data = (int*)malloc(len);
tensor->data = data;
memcpy(data,input_data.data,len);
tensor->width = input_data.width;
tensor->height = input_data.height;
tensor->channel = input_data.channel;
}
#if DEBUG
printf("tensor->width=%d,tensor->height=%d\n", tensor->width, tensor->height);
for(int c = 0; c < tensor->channel; c++){
for(int h = 0; h < tensor->height; h++) {
for(int w = 0; w < tensor->width; w++) {
printf("%d ",data[c * tensor->width * tensor->height + tensor->width * h + w]);
}
printf("\n");
}
}
printf("\n");
#endif
//output = (input - kernel + 2* pad) / stride + 1;
out_data.width = (input_data.width - weights_data.width + 2 * pad_w) / stride + 1;
out_data.height = (input_data.height - weights_data.height + 2 * pad_h) / stride + 1;
out_data.channel = 1;
len = out_data.width * out_data.height * sizeof(int);
int* output = (int*)malloc(len);
memset(output, 0, len);
out_data.data = output;
//printf("out_data.width=%d,out_data.height=%d\n", out_data.width, out_data.height);
return tensor;
}
static void conv2d(const Tensor& input_data, const Tensor& weights_data, const Tensor& out_data, const unsigned int stride, const PADDING padding) {
int* o_data = (int*)out_data.data;
int* i_data = (int*)input_data.data;
int* w_data = (int*)weights_data.data;
for(int c = 0; c < input_data.channel; c++) {
#if DEBUG
printf("c = %d\n", c);
#endif
for(int h = 0; h < input_data.height - weights_data.height + 1; h++) {
for(int w = 0; w < input_data.width - weights_data.width + 1; w++) {
int sum = 0;
for(int i = 0; i < weights_data.height; i++) {
for(int j = 0; j < weights_data.width; j++) {
int iv = i_data[c * input_data.width * input_data.height + (h + i) * input_data.width + w + j];
int wv = w_data[c * weights_data.width * weights_data.height + i * weights_data.width + j];
sum += iv * wv;
#if DEBUG
//printf("%d ", sum);
printf("%d ", iv);
#endif
}
#if DEBUG
printf("\n");
#endif
}
#if DEBUG
printf("\n");
#endif
o_data[h * out_data.width + w] = o_data[h * out_data.width + w] + sum;
}
}
}
}
#define CHANNEL (2)
#define INPUT_HEIGHT (5)
#define INPUT_WIDTH (5)
#define WEIGHTS_HEIGHT (3)
#define WEIGHTS_WIDTH (3)
int main()
{
// c*h*w shape=[c,h,w]
int input[CHANNEL][INPUT_HEIGHT][INPUT_WIDTH] = {
{{1, 0, 1, 2, 1},
{0, 2, 1, 0, 1},
{1, 1, 0, 2, 0},
{2, 2, 1, 1, 0},
{2, 0, 1, 2, 0}},
{{2, 0, 2, 1, 1},
{0, 1, 0, 0, 2},
{1, 0, 0, 2, 1},
{1, 1, 2, 1, 0},
{1, 0, 1, 1, 1}},
};
// in_c*k*k
int weights[CHANNEL][WEIGHTS_HEIGHT][WEIGHTS_WIDTH]= {
{{1, 0, 1},
{-1, 1, 0},
{0, -1, 0}},
{{-1, 0, 1},
{0, 0, 1},
{1, 1, 1}}
};
const unsigned int stride = 1;
const PADDING pad = SAME;
Tensor input_data = {CHANNEL, INPUT_WIDTH, INPUT_HEIGHT, input};
Tensor weights_data = {CHANNEL, WEIGHTS_WIDTH, WEIGHTS_HEIGHT, weights};
Tensor output_data = {CHANNEL, INPUT_WIDTH, INPUT_HEIGHT, NULL};
Tensor* padded_input = pad_input(input_data, weights_data, output_data, stride, pad);
conv2d(*padded_input, weights_data, output_data, stride, pad);
int* data = (int*)output_data.data;
for(int h = 0; h < output_data.height; h++) {
for(int w = 0; w < output_data.width; w++) {
printf("%d ", data[output_data.width * h + w]);
}
printf("\n");
}
printf("\n");
free(output_data.data);
free(padded_input->data);
free(padded_input);
return 0;
}
参考链接
- 卷积及其代码实现
- 卷积与反卷积、步长(stride)与重叠(overlap)及 output 的大小
- Tensorflow==2.0.0a0 - AttributeError: module 'tensorflow' has no attribute 'global_variables_initializer'
- tf.function和Autograph使用指南-Part 1
- Migrate your TensorFlow 1 code to TensorFlow 2
- Tensorflow卷积实现原理+手写python代码实现卷积
- pytorch的padding的理解和操作
- tensorflow padding之SAME和VALID
- Tensorflow中same padding和valid padding