什么是牛顿迭代法？
牛顿迭代法（Newton's method）又称为牛顿-拉夫逊（拉弗森）方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。
多数方程不存在求根公式，因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要。牛顿迭代法使用函数 
的泰勒级数的前面几项来寻找方程 
的根。牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程 的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根，此时线性收敛，但是可通过一些方法变成超线性收敛。（摘自百度百科）
基础数学知识
首先需要了解初等函数导数公式，后面我们需要用到这些基本的数学公式，这些基本数学知识对于初高中学生来说很简单，反倒是十几年不接触数学的上班族，都早早忘记了，尤其是当年为了考试完全死记硬背公式，完全无视推导过程的情况，如下是二次函数导数的推导过程，理解起来还是很方便的。
如下是三次函数导数的推导过程
牛顿迭代公式
设 
是 的根，选取 
作为 的初始近似值，过点 
做曲线 
的切线 
， 
(点斜式)，则 与 
轴交点的横坐标 
，称 的一近似值。过点 
做曲线 的切线，并求该切线与 轴交点的横坐标 
，称 
为 的二次近似值。重复以上过程，得 的近似值序列，其中， 
称为 的 
次近似值，上式称为牛顿迭代公式。（摘自百度百科）
以下是图解步骤：
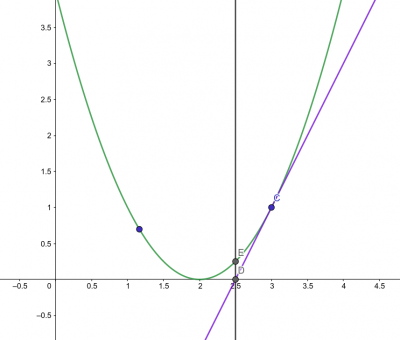
1. 以y = (x - 2) * (x - 2) 函数为例，先任意选取一点A，在曲线上做A点的切线，交X轴与B点，在B做X轴的垂线，交曲线于C点。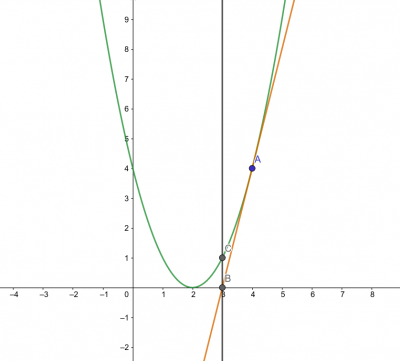 
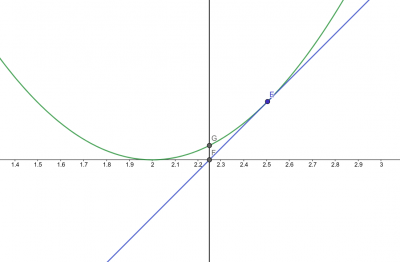
2. 在曲线上做C点的切线，交X轴与D点，在D点做X轴的垂线，交曲线于E点。我们可以看到D点比B点更加接近方程(x - 2) * (x - 2) = 0的根（x = 2）
3. 在曲线上做E点的切线，交X轴与F点，在F点做X轴的垂线，交曲线于G点。可以看到G点比D点更加接近方程的根
4. 按照这个方式不断迭代会离方程的根越来越近，以此得到近似根。
牛顿迭代法求平方根
要求是这样：输入一个数，输出其对应的平方根。
假设输入的数是 m，则其实是求一个 x 值，使其满足 x2 = m，令 f(x) = x2 - m ，其实就是求方程 f(x) = 0 的根。那么 f(x) 的导函数是 f'(x) = 2x。（这里的推导过程参考上面的介绍）
那么 f(x) 函数的曲线在 (xn，xn2 - m) 处的切线的斜率是：2xn
根据切线方程 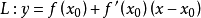我们得到：y = (xn2 - m) + 2xn (x - xn) 。
故切线与x轴的交点(y=0)是：xn+1 = (xn + m / xn ) / 2
根据牛顿迭代法，首先应该在曲线 f(x) 上任意选取一点，做切线。那么，一般我们选择 1.0，作为选取的点的横坐标(选择其他点会导致结果与标准库出现较大误差，主要集中在尾数处理上)，即 x0 = 1.0，然后根据上式进行迭代。
#include <iostream>
#include <cmath>
using namespace std;
// err 是允许的误差
const double err = 1e-8;
double NtSqrt(const double num) {
if (num < 0) {
return -1;
} else {
double root = 1.0;
// 如果原值减去近似根的平方大于误差，继续循环
while (abs(num - root * root) >= err) {
// 得到下一个近似根
root = (num / root + root) / 2.0;
}
return root;
}
}
int main(int argc, char** argv) {
double num;
cout << "请输入一个数: ";
cin >> num;
double ans = NtSqrt(num);
if (ans == -1) {
cout << "负数没有平方根" << endl;
} else {
cout << num << " 的平方根是 " << ans << endl;
}
return 0;
}
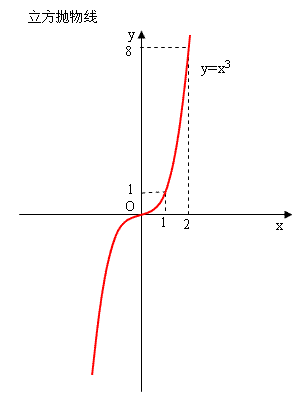
牛顿迭代法求立方根
立方函数图像如下：
要求是这样：输入一个数，输出其对应的立方根。
假设输入的数是 m，则其实是求一个 x 值，使其满足 x3 = m，令 f(x) = x3 - m ，其实就是求方程 f(x) = 0 的根。那么 f(x) 的导函数是 f'(x) = 3x2。（（这里的推导过程参考上面的介绍）
那么 f(x) 函数的曲线在 (xn，xn3 - m) 处的切线的斜率是：3xn2
根据切线方程 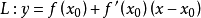我们得到：y = (xn3 - m) + 3xn2(x - xn)
故切线与x轴的交点(y=0)是：xn+1 = 2xn/3 + m/xn/xn/3
根据牛顿迭代法，首先应该在曲线 f(x) 上任意选取一点，做切线。那么，一般我们选择 1.0，作为选取的点的横坐标(选择其他点会导致结果与标准库出现较大误差，主要集中在尾数处理上)，即 x0 = 1.0，然后根据上式进行迭代。
#include <iostream>
#include <cmath>
using namespace std;
// err 是允许的误差
const double err = 1e-8;
double NtCubert(const double n) {
double r = 1.0;
// 如果原值减去近似根的立方大于误差，继续循环
while (abs(n - r * r * r) >= err) {
// 得到下一个近似根
r = 2.0 * r / 3.0 + n / r / r / 3.0;
}
return r;
}
int main(int argc, char** argv) {
double n;
cout << "请输入一个数: ";
cin >> n;
double ans = NtCubert(n);
cout << n << " 的立方根是 " << ans << endl;
return 0;
}