多项式计算
在计算机科学里,我们会经常遇到一些关于计算多项式的问题,例如计算当 ${x}=2$ 时 $2x^4 - 3x^3 + 5x^2 + x - 7$ 的值。我们首先能够想到的方法就是求出每一项的值,然后把它们全部加起来。如果多项式的阶数不高,这种方法完全可行,而且更容易理解,可是如果把这个问题推广到 $n$ 阶,即计算 $a_nx^n + a_{n-1}x^{n-1} + ··· + a_2x^2 + a_1x + a_0 $ 的值,而且当 $n$ 很大时,这种算法就显得力不从心了。
这里以 $2x^4 - 3x^3 + 5x^2 + x - 7$ 为例计算当 $x = 4$ 时的值。下面是直接求解的代码:
|
1 2 3 4 5 6 7 8 9 |
def poly_bf(coeffi_list, x): degree = len(coeffi_list) - 1 # 最高次项 result = 0 for i in range(degree+1): coeffi = coeffi_list[i]; poly = 1 for j in range(degree-i-1, -1, -1): poly *= x # 计算 x^i result += coeffi * poly return result |
直接求解的方法的复杂度等于多少呢?我们知道,计算机在计算乘法的时候的时间开销要大于加减法的时间开销,所以这里的复杂度大致看做是执行乘法运算的次数。
$T(n)=\sum_{i=1}^{n}{i+1}=2+3+\cdots+n+1=\frac{n(n+3)}{2}\in\Theta(n^2) $
最后得到时间复杂度为 $Θ(n^2)$。
霍纳法则
霍纳法则(Horner’s rule)可以将上面的多项式转化成下面的形式:
$p(x)=(\cdots(a_nx+a_{n-1})x+\cdots)x+a_0"$
假设还是计算当 $x = 4$ 时 $2x^4 - 3x^3 + 5x^2 + x - 7$ 的值,我们需要先将其转换为 $x(x(x(2x - 3) + 5) + 1) - 7$ 的形式,为了更好地呈现每一步的计算过程,我们可以构建出下面的表格:
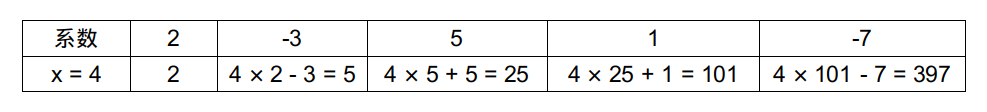
实现霍纳法则的代码非常简单,只需要用一个循环即可。
|
1 2 3 4 5 6 |
def poly_horner(coeffi_list, x): degree = len(coeffi_list) - 1 # 最高次项 result = coeffi_list[0] for i in range(1, degree+1): result = result * x + coeffi_list[i] return result |
经过霍纳法则变换的多项式只需要执行 $n$ 次乘法运算便可以得到 $n$ 阶多项式的值,所以复杂度自然就为 $Θ(n)$ 。跟直接求解相比有了明显的提升,根本原因在于我们对问题做了一个变换,使其变得更容易求解。