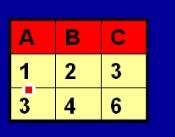
定义:在元组关系演算系统中,称{t|Q(t)}为元组演算表达式,其中t是元组变量,Q(t)是元组关系演算公式;它由原子公式和运算符组成。
我们接下来看看原子公式的三类:
1、R(t):R是关系名,t是元组变量,R(t)是元组变量,R(t)表示t是R中的元组,一般用{t|R(t)}来表示
2、t[i]Θu[j]: t,u是元组变量,Θ是算术比较运算符。t[i]Θu[j]表示命题“元组t的第i个分量与元组u的第j个分量满足比较关系Θ”
3、t[i]Θc或者cΘt[i]这里的c是常量,该公式表示“t的第i个分量与常数c满足比较关系Θ”举个很简单的例子:t[4]=3表示t的第4个分量等于3。
公式的递归定义:

这个就是咱们代数上的“且”,“并”,“非”关系,这个我相信大家都明白,这里咱们就不多说了。
接下来,我们分析例题,我们从例题中来进行更好的理解。
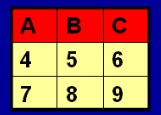
两个关系R和S:
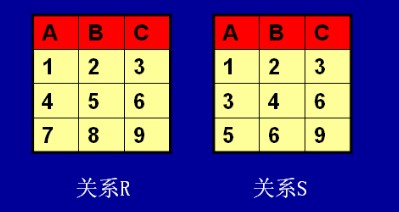
我们看R1的要求:
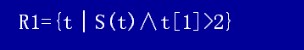
我们看到t[1]是属于S(t)中的元素,那么我们很直观的就发现,在关系S中t[1]=1<2,那么与咱们的要求t[1]>2不吻合,所以我们发现t[1]是指A这一列,那么就是说,在A这一列当中,那个数是>2的,所以我们发现了3和5,那么我们就取出了第二行和第三行:
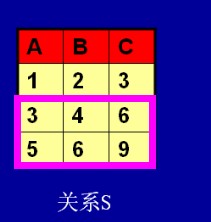
那么我们再与S(t)进行“且”的组合,就能很快的得到了我们的答案了。
我们继续看第二个要求:

我们看的出来,t是包含在R中的元组,同时要满足非S(t)代表t不能包含在S中,那么我们看到第一条:1,2,3是R中的元组,同时也是S中的元组,那么就不符合要求,我们看的出来,R中的4,5,6;7,8,9是满足我们的要求的,因为这些元组不在S中,然后我们去除了相同的元素:1、2、3.得到我们的结果:
我们继续看要求:

我们从题目的要求看的出来,t是包含在S中的,所以我们就很直观的从S中找答案;同时我们还发现u是包含在R中的。我们首先要满足这么个条件就是t[3]<u[2],我们就找出了这两列
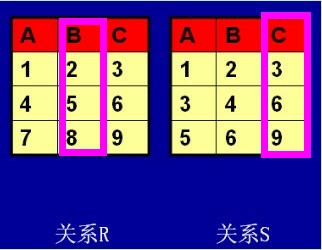
那么我们发现:u[2]有三个值,2,5,8,;其中5和8大于3,所以满足条件;那么S中的1,2,3是符合条件的。再而我们发现R中的2、5、8里边,对应的S的3,6,9里边,我们存在了8>6的元组,那么我们得出S中的3,4,6也是符合条件的要求的,那么最后我们得出的答案就是: