UWB中TOF测距法的公式推导
UWB常用测距方法有两种:飞行时间测距法(TOF)和到达时间差法(TDOA)。这里说一下TOF。
TOF
飞行时间法(Time of Flight,TOF)是一种双向测距技术,它通过测量UWB信号在基站与标签之间往返的飞行时间来计算距离。根据数学关系,一点到已知点的距离为常数,那么这点一定在以已知点为圆心,以该常数为半径的圆上。有两个已知点,就有两个交点。以三个已知点和距离作三个圆,他们交于同一个点,该点就是标签的位置。
TOF定位方式需要基站和标签往返通信,因此就造成了TOF功耗大大提高,续航时间相对较短.
TOF又分为两种:单边双向测距和双边双向测距。
单边双向测距
单边双向测距(Single-sided Two-way Ranging: SS-TWR)是对单个往返消息时间上的简单测量,设备A主动发送数据到设备B,设备B返回数据响应设备A。如下图所示:

单边双向测距的流程是这样的:设备A(Device A)主动发送(TX)数据,同时记录发送时间戳,设备B(Device B)接收到之后记录接收时间戳;延时 $T_{reply}$ 之后,设备B发送数据,同时记录发送时间戳,设备A接收数据,同时记录接收时间戳。
所以可以拿到两个时间差数据,设备A的时间差 $T_{round}$ 和设备B的时间差 $T_{reply}$ ,最终得到无线信号的飞行时间 $T_{prop}$ 如下:
$ T_{prop} = \frac{1}{2}(T_{round}-T_{reply}) $
两个差值时间都是基于本地的时钟计算得到的,本地时钟误差可以抵消,但是不同设备之间会存在微小的时钟偏移,假设设备A和B的时钟偏移分别为 $e_A$ 和 $e_B$ ,则飞行时间测量值为:
$ \hat{T}_{prop} = \frac{1}{2}[T_{round}(1+e_A)-T_{reply}(1+e_B)] $
于是测距误差如下:
$ Error = \hat{T}_{prop} - T_{prop} = \frac{1}{2}(T_{round}\cdot e_A-T_{reply}\cdot e_B) = \frac{1}{2}T_{reply}(e_A-e_B) + T_{prop}\cdot e_A $
因为 $ T_{reply} >> T_{prop} $ , 所以可以忽略后一项,得到
$ Error = \hat{T}_{prop} - T_{prop} \approx \frac{1}{2}T_{reply}(e_A-e_B) $
由此可以看出,随着 $T_{reply} $ 和时钟偏移的增加,会增加飞行时间的误差,从而使得测距不准确。因此单边双向测距(SS-TWR)并不常用,但对于特定的应用,如果对于精度要求不是很高,但是需要更短的测距时间可以采用。注意 $ T_{reply} $ 不仅仅是设备B接收到发送的时间,也包括装载数据和发送数据耗费的时间(UWB除了支持定位之外,也可以传输数据,标准可以装载128字节,扩展模式可以装载1024字节数据)。
双边双向测距
双边双向测距(Double-sided Two-way Ranging)是单边双向测距的一种扩展测距方法,记录了两个往返的时间戳,最后得到飞行时间,虽然增加了响应的时间,但会降低测距误差。
双边双向测距分为两次测距,设备A主动发起第一次测距消息,设备B响应,当设备A收到数据之后,再返回数据,最终可以得到如下四个时间差:$ T_{round1} $ 、$ T_{reply1} $ 、$ T_{round2} $ 、$ T_{reply2} $ ,如下图所示:
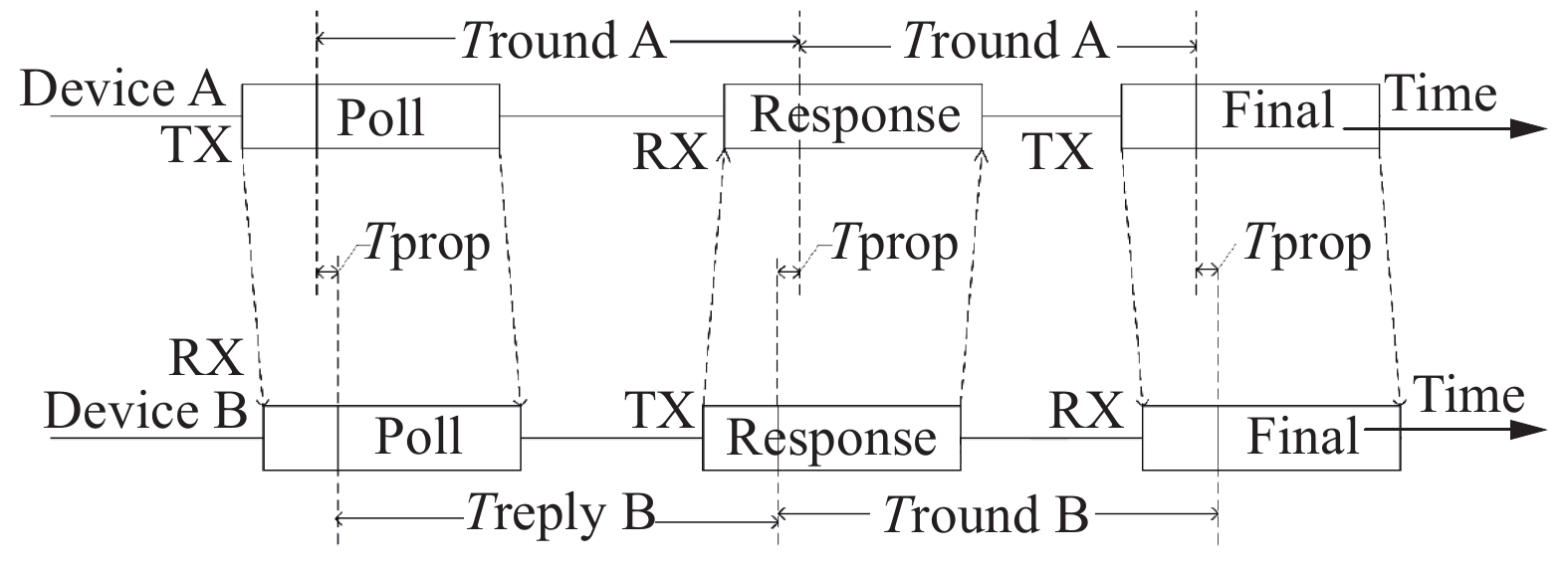
双边双向测距飞行时间计算方法:
由单边双向测距方法可得
$ T_{prop} = \frac{1}{2}(T_{round1}-T_{reply1}) $
$ T_{prop} = \frac{1}{2}(T_{round2}-T_{reply2}) $
所以
$ \begin{flalign}T_{round1} \times T_{round2} = (2T_{prop}+T_{reply1})(2T_{prop}+T_{reply2}) = 4T_{prop}^2+2T_{prop}(T_{reply1}+T_{reply2})+T_{reply1}T_{reply2} \end{flalign}$
$ \begin{flalign} T_{round1} \times T_{round2} - T_{reply1}T_{reply2} = 4T_{prop}^2+2T_{prop}(T_{reply1}+T_{reply2}) \\ = T_{prop}(4T_{prop}+2T_{reply1}+2T_{reply2}) \\ = T_{prop}(T_{round1} + T_{round2} + T_{reply1} + T_{reply2}) \end{flalign}$
于是可以得到如下计算 $ T_{prop} $ 的公式:
$ T_{prop} = \frac{T_{round1} \times T_{round2} - T_{reply1} \times T_{reply2}}{T_{round1} + T_{round2} + T_{reply1} + T_{reply2}} $
以上测距的机制是非对称的测距方法,因为他们对于响应时间不要求是相同的。下面分析双边双向测距飞行时间的误差:
$ \begin{flalign} \hat{T}_{prop} = \frac{T_{round1}(1+e_A) \times T_{round2}(1+e_B) - T_{reply1}(1+e_B) \times T_{reply2}(1+e_A)}{T_{round1}(1+e_A) + T_{round2}(1+e_B) + T_{reply1}(1+e_B) + T_{reply2}(1+e_A)} \\ = \frac{(4T_{prop}^2+2T_{prop}(T_{reply1}+T_{reply2}))(1+e_A)(1+e_B)} {4T_{prop}+2(T_{reply1}+T_{reply2})+(2T_{prop}+T_{reply1}+T_{reply2})(e_A+e_B)}\\ =\frac{2(1+e_A)(1+e_B)}{(1+e_A)+(1+e_B)}T_{prop} \end{flalign}$
于是
$ T_{prop} = \frac{(1+e_A)+(1+e_B)}{2(1+e_A)(1+e_B)}\hat{T}_{prop} $
$ \begin{flalign} Error = \hat{T}_{prop} - T_{prop} = \left(1-\frac{(1+e_A)+(1+e_B)}{2(1+e_A)(1+e_B)}\right)\hat{T}_{prop} \\ = \frac{e_A+e_B+2e_A e_B}{2(1+e_A)(1+e_B)}\hat{T}_{prop} \end{flalign} $
因为 $ e_A <<1 $,$ e_B<<1$,略去高次项,可得
$ Error \approx \frac{e_A+e_B}{2}\hat{T}_{prop} $
由此可以看出,误差仅与钟漂和飞行时间有关。
假设一个使用场景:使用20ppm的晶体,UWB的工作距离范围为300m,则无线信号空中飞行时间大概为$1 \mu s$,误差为$ 20 \times 10^{-6} \times 1 \times 10^{-6} = 20 \times 10^{-12} = 20ps $时钟误差是在ps级别的,换算为距离之后仅为6mm。
注意:响应时间是不需要相等的,也就是 $ T_{reply1} $ 不一定要等于 $ T_{reply2} $ ,这样对于MCU系统的处理带来了很多便利。
若双边双向测距方法响应时间对称,也就是 $ T_{reply1} $ 和 $ T_{reply2} $ 相等,飞行时间计算方法如下:
$ T_{prop} = \frac{1}{4}(T_{round1}-T_{reply1}+T_{round2}-T_{reply2}) $
这种方法比较简单,只是需要一些时间戳做加减法,但其难点在于,怎么保证 $T_{reply1} $ 和 $ T_{reply2} $ 是相等的。
此种方法的误差分析如下:
$ \begin{flalign} \hat{T}_{prop} = \frac{1}{4}\left[T_{round1}(1+e_A)-T_{reply1}(1+e_B)+T_{round2}(1+e_B)-T_{reply2}(1+e_A)\right] \end{flalign}$
$ \begin{flalign} Error = \hat{T}_{prop} - T_{prop} = \frac{1}{4}\left[(T_{round1}-T_{reply2})e_A +(T_{round2}-T_{reply1})e_B\right] \\ =\frac{1}{4}\left[2(e_A+e_B)T_{prop} +(e_A-e_B)(T_{reply1}-T_{reply2})\right] \end{flalign} $
因为 $ T_{reply1}-T_{reply2} >> T_{prop} $ ,可忽略$ T_{prop} $项,从而得到
$ Error \approx \frac{1}{4}(e_A-e_B)(T_{reply1}-T_{reply2})$
可见此误差与响应时间差成正比。
参考链接

