贝赛尔曲线的前世今生
贝塞尔曲线,这个命名规则一眼看上去大概是一个叫贝塞尔的数学家发明的。但,贝塞尔曲线依据的最原始的数学公式,是在1912年在数学界广为人知的伯恩斯坦多项式。简单理解,伯恩斯坦多项式可以用来证明,在[ a, b ] 区间上所有的连续函数都可以用多项式来逼近,并且收敛性很强,也就是一致收敛。再简单点,就是一个连续函数,你可以将它写成若干个伯恩斯坦多项式相加的形式,并且,随着 n→∞,这个多项式将一致收敛到原函数,这个就是伯恩斯坦斯的逼近性质。
时光荏苒岁月如梭,镜头切换到了1959年。当时就职于雪铁龙的法国数学家 Paul de Casteljau 开始对伯恩斯坦多项式进行了图形化的尝试,并且提供了一种数值稳定的德卡斯特里奥(de Casteljau) 算法。(多数理论公式是建立在大量且系统的数学建模基础之上研究的规律性成果)根据这个算法,就可以实现 通过很少的控制点,去生成复杂的平滑曲线,也就是贝塞尔曲线 。
但贝塞尔曲线的声名大噪,不得不提到1962年就职于雷诺的法国工程师皮埃尔·贝塞尔(Pierre Bézier),他使用这种方法来辅助汽车的车体工业设计(最早计算机的诞生则是为了帮助美国海军绘制弹道图),并且广泛宣传(典型的理论联系实际并获得成功的示例),因此大家称为贝塞尔曲线 。
贝赛尔曲线的数学理论
既然贝赛尔曲线的本质是通过数学计算公式去绘制平滑的曲线,那就可以通过数学工具进行实际求证以及解释说明。当然对其进行数学求证就没必要了,因为这些伟大的数学家们已经做过了,这里只是解释说明:
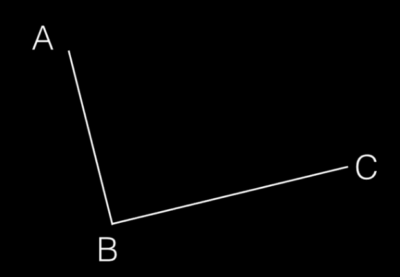
步骤一:在平面内选3个不同线的点并且依次用线段连接。
3点连线
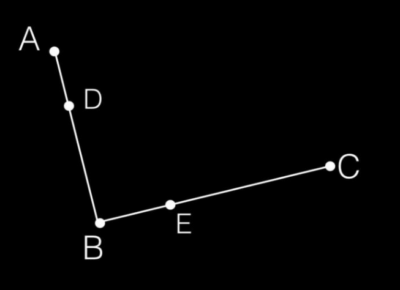
步骤二:在AB和BC线段上找出点D和点E,使得 AD/AB = BE/BC
AD/AB = BE/BC
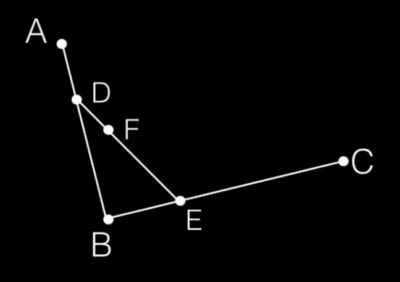
步骤三:连接DE,在DE上寻找点F,F点需要满足:DF/DE = AD/AB = BE/BC
DF/DE = AD/AB = BE/BC
步骤四:最最重要的!根据DE线段和计算公式找出所有的F点 ,记住是所有的F点,然后将其这些点连接起来。那,连接规则是什么?以上图为例,第一个连接点是A-F,第二连接点是A-F1(这个F1必须满足DF1/DE = AD/AB = BE/BC )以此类推,直到最后连接上C点,下面上一个动图加深理解:
贝塞尔曲线
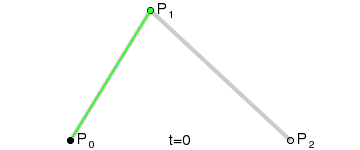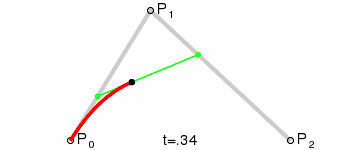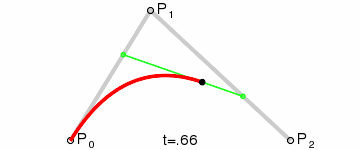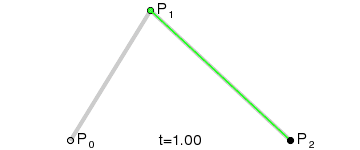
可能有些朋友还是不理解,那么这个GIF我截下其中的一张图说明,如下图:
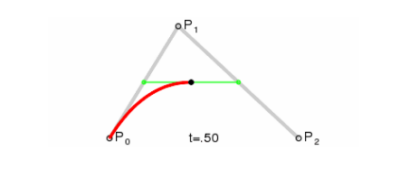
示例说明
动图里的P0、P1、P2分别代表的是上图的:P0 == A;P1 == B;P2 == C。那么这个黑色点,代表的就是F点,绿色线段的2个端点(P0-P1线段上的绿色点,代表是就是D点,P0-P2线段上的绿色点,代表是就是E点)。线段上面点的获取,必须要满足等比关系。
关于贝赛尔曲线的基本数学理论大概就是上面的内容。两个线段根据等比关系找点的贝塞尔曲线,一般也称为二阶贝塞尔曲线。
贝赛尔曲线的N阶拓展(三阶贝塞尔与N阶贝塞尔曲线)
刚才说到,上面的贝赛尔曲线一般称为二阶贝塞尔曲线,既然是二阶贝塞尔曲线,那肯定有三阶贝塞尔曲线、四阶贝赛尔曲线等等。其实三阶贝塞尔与四阶贝赛尔曲线以及N阶贝赛尔曲线曲线的规则都是一样的,都是先在线段上找点,这个点必须要满足等比关系,然后依次连接,下面是三阶贝赛尔曲线的解释说明:
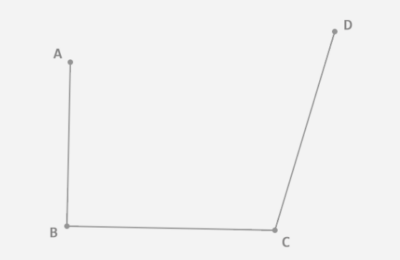
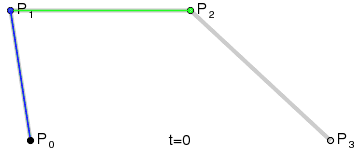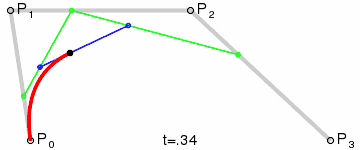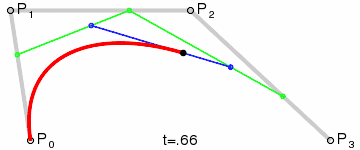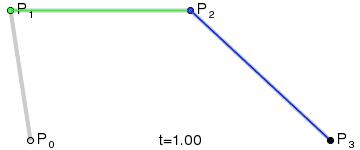
步骤一:三阶贝赛尔曲线,简单理解就是在平面内选4个不同线的点并且依次用线段连接(也就是三条线)。如下所示
四点三线
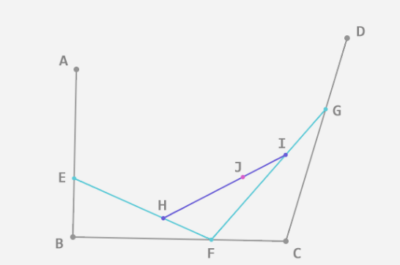
步骤二:同二阶贝塞尔曲线一样首先需要在线段上找对应的点(E、F、G),对应的点必须要符合等比的计算规则,计算规则如下:AE/AB = BF/BC = CG/CD;找到对应的点以后接着依次链接EF、FG;接着在EF、FG线段上面继续找点H、I,对应的点依旧要符合等比的计算规则,也就是 EH/EF = FI/FG;最后连接H、I线段,在HI线段上面继续找点J、点J的计算规则需要符合:EH/EF = FI/FG = HJ/HI
三阶贝赛尔曲线找点
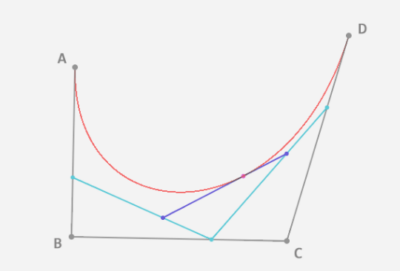
步骤三:重复步骤二的动作,找到所有的J点,依次将J点连接起来,这样最终完成了三阶贝赛尔曲线。
J点依次连线
整一个三阶贝赛尔曲线的动作加起来就是下面的一张动图:
三阶贝塞尔
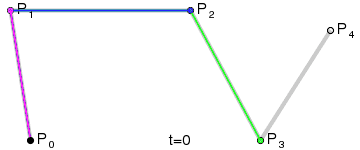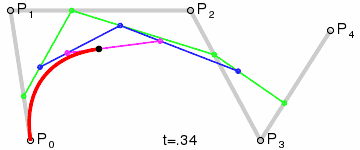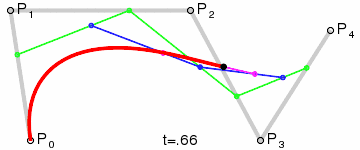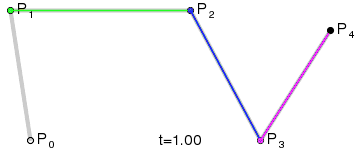
那么四阶贝赛尔曲线的实现步骤也是一样的,平面上先选取5个点(5点4线)、依次选点(满足等比关系)、依次连接、根据计算规则找到所有的点(逐个连接)。。。。。。
四阶贝赛尔曲线
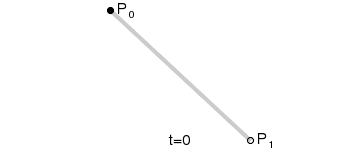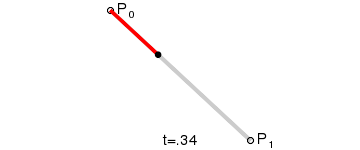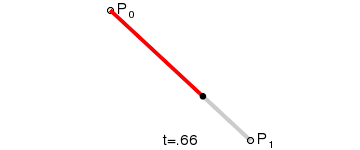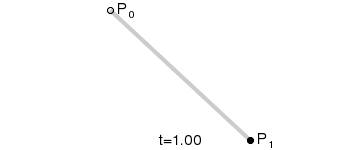
貌似都是从二阶贝塞尔曲线说起的,那么一阶贝赛尔又是怎么样的?一阶贝赛尔如图:
一阶贝赛尔
可以看到一阶贝赛尔是一条直线!
因此,N阶贝赛尔不仅可以画平滑的曲线也可以画直线,因此自定义控件画直线又多了一种可选择的方式,但是一般用贝赛尔主要是画曲线,这里只是提供了一种别的解决思路;另外,在Android属性动画,系统为我们提供了一个PathInterpolator插值器。这个PathInterpolator里面就有贝塞尔曲线的身影。有兴趣的小伙伴也可以去了解一下。
贝赛尔曲线的拟合
给定一段曲线,如何用贝塞尔曲线去拟合? 一般可以把曲线拆分成若干离散点的集合,然后要求拟合的曲线通过这些离散的数据点。
现在推导一下Bezier曲线控制点的计算过程。
曲线公式
曲 线 :$ C(u) = \displaystyle\sum_{i=0}^nB_{n,i}(u)P_i $
基 函 数 : $ B_{n,i} = \frac{ n ! }{ i ! (n−i)! } u^i ( 1 − u )^ {n − i} $
这里求解控制点,即C为已知信息,求解式中的P。
计算3次Bezier曲线控制点
曲线多项式:
$ C(u) = \displaystyle\sum_{i=0}^3 B_{3,i}(u)P_i = ( 1 − u )^3 P_0 + 3 ( 1 − u )^2 u P_1 + 3 ( 1 − u ) u^2 P_2 + u^3 P_3 , 0 ≤ u ≤ 1 $
写成矩阵方式:
$ C = B∗P $
式中:
$ B = \begin{bmatrix} 1 & 0 & 0 & 0 \\\\\frac{8}{27} & \frac{4}{9} & \frac{2}{9} & \frac{1} {27} \\\\ \frac{1} {27} & \frac{2}{9} & \frac{4}{9} & \frac{8}{27} \\\\ 0 & 0 & 0 & 1 \end{bmatrix}$
$ C = \begin{bmatrix} P_0 \\\\ P_1 \\\\P_2 \\\\P_3 \end{bmatrix}$
则得到;
$ B^{−1} C = B^{−1} B ∗ P $
$ P = B^{ − 1} C $
即可计算得到相应的样条曲线控制点。
Python验证
取点位 $ \begin{bmatrix} C_0(0,0) & C_1(0,2) & C_2(2,2) & C_3(2,0) \end{bmatrix}$
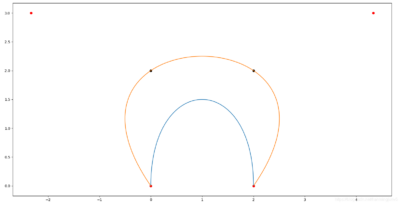
计算控制点P后,画出如下Bezier曲线:
黑色点为原始数据点;
红色点为计算得到的控制点;
蓝色曲线为由原始数据点直接拟合的Bezier 曲线;
橘黄色为由控制点拟合的Bezier 曲线;
参考链接