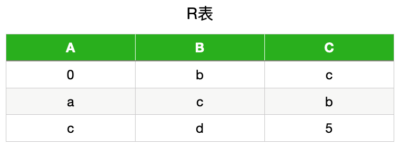
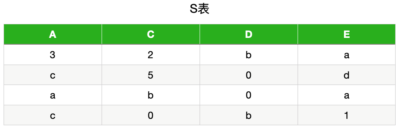
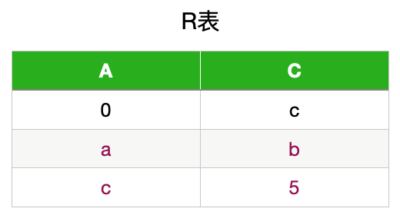
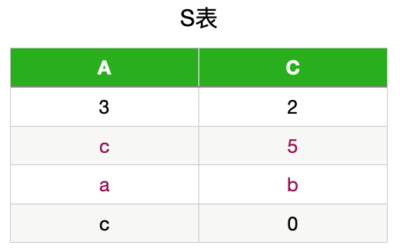
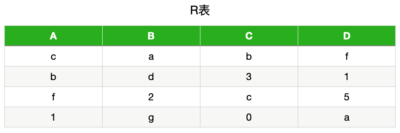
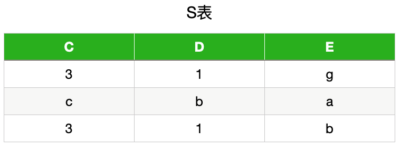
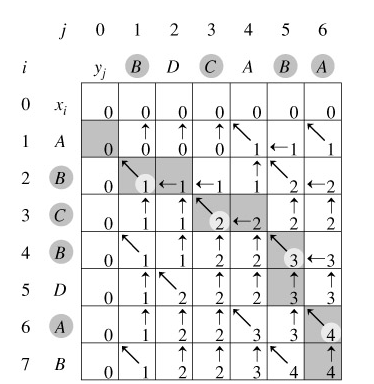
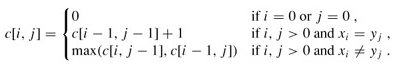大部分是对一个关系模式分解成两个模式的考察,分解为三个以上模式时无损分解和保持依赖的判断比较复杂,考的可能性不大,因此我们只对“一个关系模式分解 成两个模式”这种类型的题的相关判断做一个总结。
以下的论述都基 于这样一个前提:
R是具有函数依赖集F的关系模式,(R1 ,R2)是R的一个分解。
首先我们给出一 个看似无关却非常重要的概念:属性集的闭包 。
令α为一属性集。我们称在函数依赖集F下由α函数确定的所有属性的集合为F下α的闭包,记为α+ 。
下面给出一个计算α+的算法,该算法的输入是函数依赖集F和属性集α,输出存储在变量result中。
算法一:
result:=α;
while(result发生变化)do
for each 函数依赖β→γ in F do
begin
if β⊆result then result:=result∪γ;
end
属性集闭包的计 算有以下两个常用用途:
·判断α是否为超码,通过计算α+(α在F下的闭包),看α+ 是否包含了R中的所有属性。若是,则α为R的超码。
·通过检验是否β⊆α+,来验证函数依赖是否成立。也就是说,用属性闭包计算α+,看它是否包含β。
看一个例子 吧,2005年11月系分上午37题:
● 给定关系R(A1,A2,A3,A4)上的函数依赖集F={A1→A2,A3→A2,A2→A3,A2→A4},R的候选关键字为________。
(37)A. A1 B. A1A3 C. A1A3A4 D. A1A2A3
首先我们按照上 面的算法计算A1+ 。
result=A1,
由于A1→A2,A1⊆result,所以result=result∪A2=A1A2
由于A2→A3,A2⊆result,所以result=result∪A3=A1A2A3
由于A2→A4,A2⊆result,所以result=result∪A3=A1A2A3A4
由于A3→A2,A3⊆result,所以result=result∪A2=A1A2A3A4
通过计算我们看 到,A1+ =result={A1A2A3A4},所以A1是R的超码,理所当然是R的候选关键字。此题选A 。
好了,有了前面的铺垫,我们进入正题。
无损分解的判断 。
如果R1∩R2是R1或R2的超码,则R上的分解(R1,R2)是无损分解。这是一个充分条件,当所有的约束都是函数依赖时它才是必要条件(例如多值依赖 就是一种非函数依赖的约束),不过这已经足够了。
保持依赖的判断 。
如果F上的每一个函数依赖都在其分解后的某一个关系上成立,则这个分解是保持依赖的(这是一个充分条件)。
如果上述判断失败,并不能断言分解不是保持依赖的,还要使用下面的通用方法来做进一步判断。
该方法的表述如下:
算法二:
对F上的每一个α→β使用下面的过程:
result:=α;
while(result发生变化)do
for each 分解后的Ri
t=(result∩Ri)+ ∩Ri
result=result∪t
这里的属性闭包是在函数依赖集F下计算出来的。如果result中包含了β的所有属性,则函数依赖α→β。分解是保持依赖的当且仅当上述过程中F的所有依 赖都被保持。
下面给出一个例题,2006年5月系分上午43题:
●设关系模式R<U, F>,其中U={A, B, C, D, E},F={A→BC,C→D,BC→E,E→A},则分解ρ={R1(ABCE),R2(CD)}满足 (43) 。
(43) A.具有无损连接性、保持函数依赖
B.不具有无损连接性、保持函数依赖
C.具有无损连接性、不保持函数依赖
D.不具有无损连接性、不保持函数依赖
先做无损链接的判断。R1∩R2={C},计算C+。
Result=C
由于C→D,C∈result,所以result=result∪D=CD
可见C是R2的超码,该分解是一个无损分解。
再做保持依赖的 判断。
A→BC,BC→E, E→A都在R1上成立(也就是说每一个函数依赖左右两边的属性都在R1中),C→D在R2上成立,因此给分解是保持依赖的。
选A。
再看一个复杂点的例题。2007年5月数工40-41题。
●给定关系模式R<U, F>,U={A, B, C, D, E},F={B→A,D→A,A→E,AC→B},其候选关键字为
(40) ,则分解ρ={R1(ABCE),R2(CD)}满足 (41) 。
(40) A.ABD
B.ABE
C.ACD
D.CD
(41) A.具有无损连接性、保持函数依赖
B.不具有无损连接性、保持函数依赖
C.具有无损连接性、不保持函数依赖
D.不具有无损连接性、不保持函数依赖
看见了吧,和前 面一题多么的相像!
对于第一问,分别计算ABCD四个选项的闭包,
(ABD)+ = { ABDE }
(ABE)+ = { ABE }
(ACD)+ = { ABCDE }
(CD)+ = { ABCDE }
选D。
再看第二问。
先做无损链接的判断。R1∩R2={C},计算C+。
result=C
因此C既不是R1也不是R2的超码,该分解不具有无损分解性。
再做保持依赖的 判断。
B→A,A→E,AC→B在R1上成立,D→A在R1和R2上都不成立,因此需做进一步判断。
由于B→A,A→E,AC→B都是被保持的(因为它们的元素都在R1中),因此我们要判断的是D→A是不是也被保持。
对于D→A应用 算法二:
result=D
对R1,result∩R1=ф(空集,找不到空集的符号,就用这个表示吧),t=ф,result=D
再对R2,result∩R2=D,D+ =ADE ,t=D+ ∩R2=D,result=D
一个循环后result未发生变化,因此最后result=D,并未包含A,所以D→A未被保持,该分解不是保持依赖的。
选D。