深海游弋的鱼 – 默默的点滴

贝塞尔曲线

贝赛尔曲线的前世今生

贝塞尔曲线，这个命名规则一眼看上去大概是一个叫贝塞尔的数学家发明的。但，贝塞尔曲线依据的最原始的数学公式，是在1912年在数学界广为人知的伯恩斯坦多项式。简单理解，伯恩斯坦多项式可以用来证明，在[ a, b ] 区间上所有的连续函数都可以用多项式来逼近，并且收敛性很强，也就是一致收敛。再简单点，就是一个连续函数，你可以将它写成若干个伯恩斯坦多项式相加的形式，并且，随着 n→∞，这个多项式将一致收敛到原函数，这个就是伯恩斯坦斯的逼近性质。

时光荏苒岁月如梭，镜头切换到了1959年。当时就职于雪铁龙的法国数学家 Paul de Casteljau 开始对伯恩斯坦多项式进行了图形化的尝试，并且提供了一种数值稳定的德卡斯特里奥（de Casteljau）算法。（多数理论公式是建立在大量且系统的数学建模基础之上研究的规律性成果）根据这个算法，就可以实现 通过很少的控制点，去生成复杂的平滑曲线，也就是贝塞尔曲线。

但贝塞尔曲线的声名大噪，不得不提到1962年就职于雷诺的法国工程师皮埃尔·贝塞尔（Pierre Bézier），他使用这种方法来辅助汽车的车体工业设计（最早计算机的诞生则是为了帮助美国海军绘制弹道图），并且广泛宣传（典型的理论联系实际并获得成功的示例），因此大家称为贝塞尔曲线。

贝赛尔曲线的数学理论

既然贝赛尔曲线的本质是通过数学计算公式去绘制平滑的曲线，那就可以通过数学工具进行实际求证以及解释说明。当然对其进行数学求证就没必要了，因为这些伟大的数学家们已经做过了，这里只是解释说明：

步骤一：在平面内选3个不同线的点并且依次用线段连接。

3点连线
步骤二：在AB和BC线段上找出点D和点E，使得 AD/AB = BE/BC

AD/AB = BE/BC
步骤三：连接DE，在DE上寻找点F，F点需要满足：DF/DE = AD/AB = BE/BC

DF/DE = AD/AB = BE/BC
步骤四：最最重要的！根据DE线段和计算公式找出所有的F点，记住是所有的F点，然后将其这些点连接起来。那，连接规则是什么？以上图为例，第一个连接点是A-F，第二连接点是A-F1（这个F1必须满足DF1/DE = AD/AB = BE/BC）以此类推，直到最后连接上C点，下面上一个动图加深理解：

贝塞尔曲线

可能有些朋友还是不理解，那么这个GIF我截下其中的一张图说明，如下图：

示例说明

动图里的P0、P1、P2分别代表的是上图的：P0 == A；P1 == B；P2 == C。那么这个黑色点，代表的就是F点，绿色线段的2个端点（P0-P1线段上的绿色点，代表是就是D点，P0-P2线段上的绿色点，代表是就是E点）。线段上面点的获取，必须要满足等比关系。

关于贝赛尔曲线的基本数学理论大概就是上面的内容。两个线段根据等比关系找点的贝塞尔曲线，一般也称为二阶贝塞尔曲线。

贝赛尔曲线的N阶拓展（三阶贝塞尔与N阶贝塞尔曲线）

刚才说到，上面的贝赛尔曲线一般称为二阶贝塞尔曲线，既然是二阶贝塞尔曲线，那肯定有三阶贝塞尔曲线、四阶贝赛尔曲线等等。其实三阶贝塞尔与四阶贝赛尔曲线以及N阶贝赛尔曲线曲线的规则都是一样的，都是先在线段上找点，这个点必须要满足等比关系，然后依次连接，下面是三阶贝赛尔曲线的解释说明：

步骤一：三阶贝赛尔曲线，简单理解就是在平面内选4个不同线的点并且依次用线段连接（也就是三条线）。如下所示

四点三线
步骤二：同二阶贝塞尔曲线一样首先需要在线段上找对应的点（E、F、G），对应的点必须要符合等比的计算规则，计算规则如下：AE/AB = BF/BC = CG/CD；找到对应的点以后接着依次链接EF、FG；接着在EF、FG线段上面继续找点H、I，对应的点依旧要符合等比的计算规则，也就是 EH/EF = FI/FG；最后连接H、I线段，在HI线段上面继续找点J、点J的计算规则需要符合：EH/EF = FI/FG = HJ/HI

三阶贝赛尔曲线找点
步骤三：重复步骤二的动作，找到所有的J点，依次将J点连接起来，这样最终完成了三阶贝赛尔曲线。

J点依次连线

整一个三阶贝赛尔曲线的动作加起来就是下面的一张动图：

那么四阶贝赛尔曲线的实现步骤也是一样的，平面上先选取5个点（5点4线）、依次选点（满足等比关系）、依次连接、根据计算规则找到所有的点（逐个连接）。。。。。。

貌似都是从二阶贝塞尔曲线说起的，那么一阶贝赛尔又是怎么样的？一阶贝赛尔如图：

可以看到一阶贝赛尔是一条直线！

因此，N阶贝赛尔不仅可以画平滑的曲线也可以画直线，因此自定义控件画直线又多了一种可选择的方式，但是一般用贝赛尔主要是画曲线，这里只是提供了一种别的解决思路；另外，在Android属性动画，系统为我们提供了一个PathInterpolator插值器。这个PathInterpolator里面就有贝塞尔曲线的身影。有兴趣的小伙伴也可以去了解一下。

贝赛尔曲线的拟合

给定一段曲线，如何用贝塞尔曲线去拟合? 一般可以把曲线拆分成若干离散点的集合，然后要求拟合的曲线通过这些离散的数据点。

现在推导一下Bezier曲线控制点的计算过程。

曲线公式

曲线： $C (u) = \sum_{i = 0}^{n} B_{n, i} (u) P_{i}$

基函数： $B_{n, i} = \frac{n!}{i! (n - i)!} u^{i} (1 - u)^{n - i}$

这里求解控制点，即C为已知信息，求解式中的P。

计算3次Bezier曲线控制点

曲线多项式：

$C (u) = \sum_{i = 0}^{3} B_{3, i} (u) P_{i} = (1 - u)^{3} P_{0} + 3 (1 - u)^{2} u P_{1} + 3 (1 - u) u^{2} P_{2} + u^{3} P_{3}, 0 \leq u \leq 1$

写成矩阵方式：

$C = B * P$

式中：

$B = [\begin{matrix} 1 & 0 & 0 & 0 \\ \frac{8}{27} & \frac{4}{9} & \frac{2}{9} & \frac{1}{27} \\ \frac{1}{27} & \frac{2}{9} & \frac{4}{9} & \frac{8}{27} \\ 0 & 0 & 0 & 1 \end{matrix}]$

$C = [\begin{matrix} P_{0} \\ P_{1} \\ P_{2} \\ P_{3} \end{matrix}]$

则得到;

$B^{- 1} C = B^{- 1} B * P$

$P = B^{- 1} C$

即可计算得到相应的样条曲线控制点。

Python验证

取点位 $[\begin{matrix} C_{0} (0, 0) & C_{1} (0, 2) & C_{2} (2, 2) & C_{3} (2, 0) \end{matrix}]$

计算控制点P后，画出如下Bezier曲线：

黑色点为原始数据点；
红色点为计算得到的控制点；
蓝色曲线为由原始数据点直接拟合的Bezier曲线；
橘黄色为由控制点拟合的Bezier曲线；

黑色点为原始数据点；

红色点为计算得到的控制点；

蓝色曲线为由原始数据点直接拟合的Bezier曲线；

橘黄色为由控制点拟合的Bezier曲线；

参考链接

Flutter绘制贝塞尔曲线、折线、柱状图，支持触摸

之前写过一篇Android原生绘制曲线图的博客，动画效果不要太丝滑，那么现在到了Flutter，该如何实现类似的效果呢？如果你熟悉Android的Canvas,那么恭喜你, 你将很快上手Flutter的Canvas绘制各种图形，因为实现方式基本上与Android是一模一样。

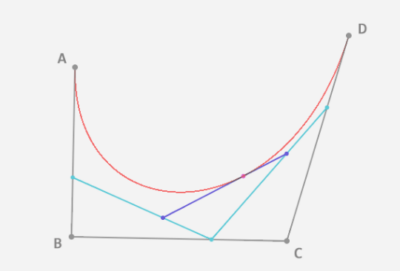
先看下要实现的基本效果：

Flutter中如果想要自定义绘制，那么你需要用到 CustomPaint 和 CustomPainter ; CustomPaint是Widget的子类，先来看下构造方法

const CustomPaint({
    Key key,
    this.painter,
    this.foregroundPainter,
    this.size = Size.zero,
    this.isComplex = false,
    this.willChange = false,
    Widget child,
  }) :super(key: key, child: child);

const CustomPaint({

Key key,

this.painter,

this.foregroundPainter,

this.size = Size.zero,

this.isComplex = false,

this.willChange = false,

Widget child,

}) :super(key: key, child: child);

我们只需要关心三个参数，painter，foregroundPainter 和 child ，这里需要说明一下，painter 是绘制的 backgroud 层，而child 是在backgroud之上绘制，foregroundPainter 是在 child 之上绘制，所以这里就有了个层级关系，这跟android里面的backgroud与foreground是一个意思，那这两个painter的应用场景是什么呢？假如你只是单纯的想绘制一个图形，只用painter就可以了，但是如果你想给绘制区域添加一个背景（颜色，图片，等等），这时候如果使用 painter是会有问题的，painter的绘制会被child 层覆盖掉，此时你只需要将painter替换成foregroundPainter,然会颜色或者图片传递给child即可。

如果是Android绘制几何图形，应该是重写View的onLayout() 和 onDraw方法。但是Flutter实现绘制，必须继承CustomPainter并重写 paint(Canvas canvas, Size size)和 shouldRepaint (CustomPainter oldDelegate)方法，第一个参数canvas就是我们绘制的画布了（跟Android一模一样），paint第二个参数Size就是上面CustomPaint构造方法传入的size, 决定绘制区域的宽高信息

既然Size已经确定了，现在就定义下绘制区域的边界,一般我做类似的UI，都会定义一个最基本的padding, 一般取值为16 ，因为绘制的内容与坐标轴之间需要找到一个基准线，这样更容易绘制，而且调试边距也很灵活

double startX, endX, startY, endY;//定义绘制区域的边界
static const double basePadding = 16; //默认的边距
double fixedHeight, fixedWidth; //去除padding后曲线的真实宽高
bool isShowXyRuler; //是否显示xy刻度
List<ChatBean> chatBeans;//数据源
 
class ChatBean {
  String x;
  double y;
  int millisSeconds;
  Color color;
 
  ChatBean({@required this.x, @required this.y, this.millisSeconds, this.color});
}

double startX, endX, startY, endY;//定义绘制区域的边界

static const double basePadding = 16; //默认的边距

double fixedHeight, fixedWidth; //去除padding后曲线的真实宽高

bool isShowXyRuler; //是否显示xy刻度

List<ChatBean> chatBeans;//数据源

class ChatBean {

String x;

double y;

int millisSeconds;

Color color;

ChatBean({@required this.x, @required this.y, this.millisSeconds, this.color});

}

然后在paint()方法中拿到Size,确定绘制区域的坐标

///计算边界
  void initBorder(Size size) {
    print('size - - > $size');
    this.size = size;
    startX = yNum > 0 ? basePadding * 2.5 : basePadding * 2; //预留出y轴刻度值所占的空间
    endX = size.width - basePadding * 2;
    startY = size.height - (isShowXyRuler ? basePadding * 3 : basePadding);
    endY = basePadding * 2;
    fixedHeight = startY - endY;
    fixedWidth = endX - startX;
    maxMin = calculateMaxMin(chatBeans);
  }

///计算边界

void initBorder(Size size) {

print('size - - > $size');

this.size = size;

startX = yNum > 0 ? basePadding * 2.5 : basePadding * 2; //预留出y轴刻度值所占的空间

endX = size.width - basePadding * 2;

startY = size.height - (isShowXyRuler ? basePadding * 3 : basePadding);

endY = basePadding * 2;

fixedHeight = startY - endY;

fixedWidth = endX - startX;

maxMin = calculateMaxMin(chatBeans);

}

maxMin是定义存储曲线中最大值和最小值的

///计算极值 最大值,最小值
  List<double> calculateMaxMin(List<ChatBean> chatBeans) {
    if (chatBeans == null || chatBeans.length == 0) return [0, 0];
    double max = 0.0, min = 0.0;
    for (ChatBean bean in chatBeans) {
      if (max < bean.y) {
        max = bean.y;
      }
      if (min > bean.y) {
        min = bean.y;
      }
    }
    return [max, min];
  }

///计算极值最大值,最小值

List<double> calculateMaxMin(List<ChatBean> chatBeans) {

if (chatBeans == null || chatBeans.length == 0) return [0, 0];

double max = 0.0, min = 0.0;

for (ChatBean bean in chatBeans) {

if (max < bean.y) {

max = bean.y;

}

if (min > bean.y) {

min = bean.y;

}

return [max, min];

}

初始化画笔 .. 是dart中的独特语法，代表使用对象的返回值调用属性或方法

var paint = Paint()
      ..isAntiAlias = true//抗锯齿
      ..strokeWidth = 2
      ..strokeCap = StrokeCap.round//折线连接处圆滑处理
      ..color = xyColor
      ..style = PaintingStyle.stroke;//描边

var paint = Paint()

..isAntiAlias = true//抗锯齿

..strokeWidth = 2

..strokeCap = StrokeCap.round//折线连接处圆滑处理

..color = xyColor

..style = PaintingStyle.stroke;//描边

绘制坐标轴，这里在确定好的边界基础上再次xy轴横向和纵向各自增加一倍的padding,不然显得太紧凑

canvas.drawLine(Offset(startX, startY),Offset(endX + basePadding, startY), paint); //x轴

canvas.drawLine(Offset(startX, startY),Offset(startX, endY - basePadding), paint); //y轴

canvas.drawLine(Offset(startX, startY),Offset(endX + basePadding, startY), paint); //x轴

canvas.drawLine(Offset(startX, startY),Offset(startX, endY - basePadding), paint); //y轴

绘制 X 轴刻度，定义为最多绘制7组数据，rulerWidth就是刻度的长度定义为8

int length = chatBeans.length > 7 ? 7 : chatBeans.length; //最多绘制7个
double DW = fixedWidth / (length - 1); //两个点之间的x方向距离
double DH = fixedHeight / (length - 1); //两个点之间的y方向距离
for (int i = 0; i < length; i++) {
     ///绘制x轴文本
     TextPainter(
            textAlign: TextAlign.center,
            ellipsis: '.',
            text: TextSpan(
                text: chatBeans[i].x,
                style: TextStyle(color: fontColor, fontSize: fontSize)),
            textDirection: TextDirection.ltr)
          ..layout(minWidth: 40, maxWidth: 40)
          ..paint(canvas, Offset(startX + DW * i - 20, startY + basePadding));
 
      ///x轴刻度
      canvas.drawLine(Offset(startX + DW * i, startY),Offset(startX + DW * i, startY - rulerWidth), paint);
   }

int length = chatBeans.length > 7 ? 7 : chatBeans.length; //最多绘制7个

double DW = fixedWidth / (length - 1); //两个点之间的x方向距离

double DH = fixedHeight / (length - 1); //两个点之间的y方向距离

for (int i = 0; i < length; i++) {

///绘制x轴文本

TextPainter(

textAlign: TextAlign.center,

ellipsis: '.',

text: TextSpan(

text: chatBeans[i].x,

style: TextStyle(color: fontColor, fontSize: fontSize)),

textDirection: TextDirection.ltr)

..layout(minWidth: 40, maxWidth: 40)

..paint(canvas, Offset(startX + DW * i - 20, startY + basePadding));

///x轴刻度

canvas.drawLine(Offset(startX + DW * i, startY),Offset(startX + DW * i, startY - rulerWidth), paint);

}

这里要说明一点，Flutter绘制文本，并不能像android那样调用canvas.drawText(), 而是通过TextPainter来渲染的，

构造TextPainter 你必须指定文字的方向 textDirection 和宽度 layout ,最后调用paint方法，指定坐标进行绘制

绘制 Y 轴刻度，y轴的刻度数量并不需要跟随数据源的长度，只需要按照一定数量(yNum )平分y轴最大值即可

      int yLength = yNum + 1; //包含原点,所以 +1
      double dValue = maxMin[0] / yNum; //一段对应的值
      double dV = fixedHeight / yNum; //一段对应的高度
      for (int i = 0; i < yLength; i++) {
        ///绘制y轴文本，保留1位小数
        var yValue = (dValue * i).toStringAsFixed(isShowFloat ? 1 : 0);
        TextPainter(
            textAlign: TextAlign.center,
            ellipsis: '.',
            maxLines: 1,
            text: TextSpan(  
                text: '$yValue',
                style: TextStyle(color: fontColor, fontSize: fontSize)),
            textDirection: TextDirection.rtl)
          ..layout(minWidth: 40, maxWidth: 40)
          ..paint(canvas, Offset(startX - 40, startY - dV * i - fontSize / 2));
 
        ///y轴刻度
        canvas.drawLine(Offset(startX, startY - dV * (i)),Offset(startX + rulerWidth, startY - dV * (i)), paint);
      }

int yLength = yNum + 1; //包含原点,所以 +1

double dValue = maxMin[0] / yNum; //一段对应的值

double dV = fixedHeight / yNum; //一段对应的高度

for (int i = 0; i < yLength; i++) {

///绘制y轴文本，保留1位小数

var yValue = (dValue * i).toStringAsFixed(isShowFloat ? 1 : 0);

TextPainter(

textAlign: TextAlign.center,

ellipsis: '.',

maxLines: 1,

text: TextSpan(

text: '$yValue',

style: TextStyle(color: fontColor, fontSize: fontSize)),

textDirection: TextDirection.rtl)

..layout(minWidth: 40, maxWidth: 40)

..paint(canvas, Offset(startX - 40, startY - dV * i - fontSize / 2));

///y轴刻度

canvas.drawLine(Offset(startX, startY - dV * (i)),Offset(startX + rulerWidth, startY - dV * (i)), paint);

}

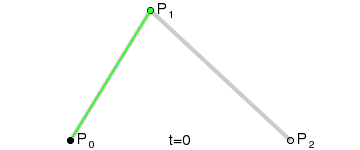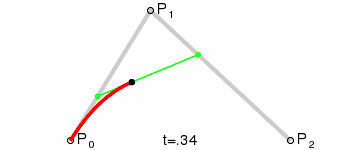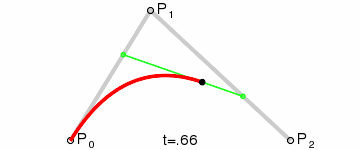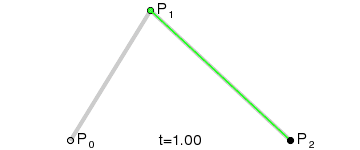
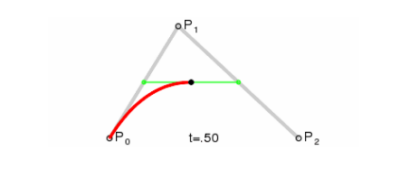
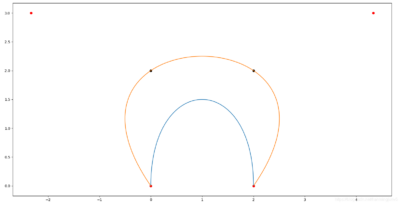
现在坐标轴和刻度已经绘制完成了，基本上与原生一致，只是代码方式有些区别，接下来的曲线也是一模一样的，绘制贝塞尔曲线其实也不难，主要是找到起点和两个坐标之间的辅助点，贝塞尔曲线的原理可以参考这里

path.cubicTo(double x1, double y1, double x2, double y2, double x3, double y3)

1	path.cubicTo(double x1, double y1, double x2, double y2, double x3, double y3)

path = Path();
double preX, preY, currentX, currentY;
int length = chatBeans.length > 7 ? 7 : chatBeans.length;
double W = fixedWidth / (length - 1); //两个点之间的x方向距离

path = Path();

double preX, preY, currentX, currentY;

int length = chatBeans.length > 7 ? 7 : chatBeans.length;

double W = fixedWidth / (length - 1); //两个点之间的x方向距离

遍历数据源的第一个元素时，需要做个判断，index=0时，需要将path move到此处

if (i == 0) {
     path.moveTo(startX, (startY - chatBeans[i].y / maxMin[0] * fixedHeight));
     continue;
   }

if (i == 0) {

path.moveTo(startX, (startY - chatBeans[i].y / maxMin[0] * fixedHeight));

continue;

}

添加后面的坐标时，需要找辅助点

currentX = startX + W * i;
preX = startX + W * (i - 1);
 
preY = (startY - chatBeans[i - 1].y / maxMin[0] * fixedHeight);
currentY = (startY - chatBeans[i].y / maxMin[0] * fixedHeight);
 
path.cubicTo(
              (preX + currentX) / 2, preY,
              (preX + currentX) / 2, currentY,
              currentX, currentY
            );

currentX = startX + W * i;

preX = startX + W * (i - 1);

preY = (startY - chatBeans[i - 1].y / maxMin[0] * fixedHeight);

currentY = (startY - chatBeans[i].y / maxMin[0] * fixedHeight);

path.cubicTo(

(preX + currentX) / 2, preY,

(preX + currentX) / 2, currentY,

currentX, currentY

);

如果是要画折线而非曲线，第一步还是path.moveTo ，折线不需要找辅助点，所以后续可以直接添加坐标，path.lineTo

最后将path绘制出来

canvas.drawPath(newPath, paint);

1	canvas.drawPath(newPath, paint);

虽然曲线已经成功绘制，但是这样显得很枯燥，如果可以看到绘制过程那就会更加有趣味性，这时候就需要通过动画来更新曲线的path的长度了，一般Android中我会用ValueAnimator.ofFloat(start ,end ) 来开启一个动画 ,在Flutter中，动画也是非常简单实用

_controller = AnimationController(vsync: this, duration: widget.duration);
      Tween(begin: 0.0, end: widget.duration.inMilliseconds.toDouble())
          .animate(_controller)
            ..addStatusListener((status) {
              if (status == AnimationStatus.completed) {
                print('绘制完成');
              }
            })
            ..addListener(() {
              _value = _controller.value;//当前动画值
              setState(() {});
            });
      _controller.forward();

_controller = AnimationController(vsync: this, duration: widget.duration);

Tween(begin: 0.0, end: widget.duration.inMilliseconds.toDouble())

.animate(_controller)

..addStatusListener((status) {

if (status == AnimationStatus.completed) {

print('绘制完成');

}

})

..addListener(() {

_value = _controller.value;//当前动画值

setState(() {});

});

_controller.forward();

动画执行过程中，我们会及时获取到当前的动画进度 _value, 此时就需要一段完整的path跟随动画值等比绘制了，之前在Android中我们可以用 PathMeasure 来测量path ，然后根据动画进度不断地截取，就实现了像贪吃蛇一样的效果，但是在Flutter中，我并没有找到PathMeasure 这个类，相反的，PathMeasure 在Flutter竟然是个私有的类 _PathMeasure ，经过一通百度和 Google，也没有找到类似的案例。难道没有人给造轮子，就必须要停止我前进的步伐了嘛，不急，显然Path这个类里面有很多方法，就这样我走上了一条反复测试的不归路...

幸运的是，在翻阅了Google 官方Flutter Api 后，终于找到了突破口

哈哈，藏得还挺深呐，就是这个 PathMetrics 类，path.computeMetrics() 的返回值，是用来将path解析成矩阵的一个工具

var pathMetrics = path.computeMetrics(forceClosed: false);

1	var pathMetrics = path.computeMetrics(forceClosed: false);

有个参数 forceClosed ，表示是否要连接path的起始点，我们这里当然不要啦，computeMetrics方法返回的是PathMetrics对象，调用 toList ()，可以获取到多个path组成的 List<PathMetric> ; 集合中的每个元素代表一段path的矩阵，奇怪，为什么是多个path 呢？？？

当时我也是懵着猜测的，历史总是惊人的相似，被我给猜对了，不晓得你们有没有发现，Path有个方法可以添加多个Path ,

path.addPath(path, offset);

1	path.addPath(path, offset);

当我每调用一次 addPath() 或者 moveTo()，lsit . length就增加1，所以上面提到的多个path的集合就不难理解了，因为我们这里只有一个path，所以我们的 list 中只有一个元素 , 元素中包含一段path, 现在我们获取到了描述path的矩阵PathMetric

PathMetric.length 就是这段path的长度了，唉，为了找到你，我容易吗！

另外还有个关键的方法，可以将pathMetric按照给定的位置区间截取，最后返回这段path, 这就跟Android中的PathMeasure.getSegment()是一样

extractPath（double start， double end，{ bool startWithMoveTo：true }） → Path
给定起始和停止距离，返回中间段。

1 2	extractPath（double start， double end，{ bool startWithMoveTo：true }） → Path 给定起始和停止距离，返回中间段。

现在是时候将前面获取到的当前动画值 value 用起来了，找到当前path的length乘以value即是当前path的最新长度

var pathMetrics = path.computeMetrics(forceClosed: true);
var list = pathMetrics.toList();
var length = value * list.length.toInt();
Path newPath = new Path();
for (int i = 0; i < length; i++) {
     var extractPath = list[i].extractPath(0, list[i].length * value, startWithMoveTo: true);
      newPath.addPath(extractPath, Offset(0, 0));
    }
 canvas.drawPath(newPath, paint);

var pathMetrics = path.computeMetrics(forceClosed: true);

var list = pathMetrics.toList();

var length = value * list.length.toInt();

Path newPath = new Path();

for (int i = 0; i < length; i++) {

var extractPath = list[i].extractPath(0, list[i].length * value, startWithMoveTo: true);

newPath.addPath(extractPath, Offset(0, 0));

}

canvas.drawPath(newPath, paint);

走到这里，好像跨过了山和大海，得了，困死了，睡了、睡了...

现在曲线和折线都已经绘制完成了，不过刚开始的demo里还有个渐变色的部分没有完成，貌似有了渐变色以后，显得不那么单调了，其实，我们绘图所用到的Paint还有一个属性shader，可以绘制线条或区域的渐变色，LinearGradient可实现线性渐变的效果，默认为从左到右绘制，你可以通过begin和end属性自定义绘制的方向，我们这里需要指定为从上至下，并且颜色类型为数组的形式，所以你可以传入多个颜色值来绘制

var shader = LinearGradient(
              begin: Alignment.topCenter,
              end: Alignment.bottomCenter,
              tileMode: TileMode.clamp,
              colors: shaderColors)
          .createShader(Rect.fromLTRB(startX, endY, startX, startY));

var shader = LinearGradient(

begin: Alignment.topCenter,

end: Alignment.bottomCenter,

tileMode: TileMode.clamp,

colors: shaderColors)

.createShader(Rect.fromLTRB(startX, endY, startX, startY));

值得注意的是，通过 createShader的方式创建shader，你需要指定绘制区域的边界，我们这里要实现的是从上至下，所以就以y轴为基准，指定从上至下的绘制方向

既然是绘制渐变色，所以画笔的样式必须设置为填充状态

Paint shadowPaint = new Paint();
      shadowPaint
        ..shader = shader
        ..isAntiAlias = true
        ..style = PaintingStyle.fill;

Paint shadowPaint = new Paint();

shadowPaint

..shader = shader

..isAntiAlias = true

..style = PaintingStyle.fill;

另外，渐变色的区域我们是通过path来指定上面的边界的，所以我们还需要指定path下面部分的起点和终点，这样形成一个闭环，才能确定出完整的区域

///从path的最后一个点连接起始点，形成一个闭环
      shadowPath
        ..lineTo(startX + fixedWidth * value, startY)
        ..lineTo(startX, startY)
        ..close();
      canvas..drawPath(shadowPath, shadowPaint);

///从path的最后一个点连接起始点，形成一个闭环

shadowPath

..lineTo(startX + fixedWidth * value, startY)

..lineTo(startX, startY)

..close();

canvas..drawPath(shadowPath, shadowPaint);

至此，即可实现带有渐变色的曲线或者折线，也许你有个疑问，画折线为什么也要用path呢，不是可以直接drawLine吗？机智如我，添加到path以后，可以更方便的绘制，添加动画也很方便

另附上最终的实现效果，至于触摸操作就不打算阐述了，可以参考以下代码

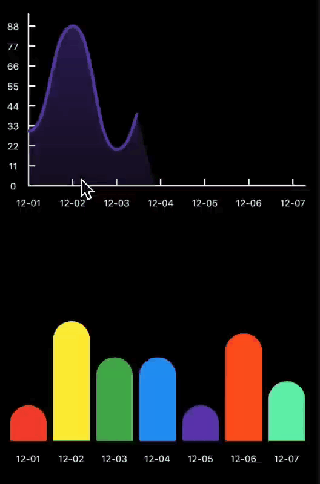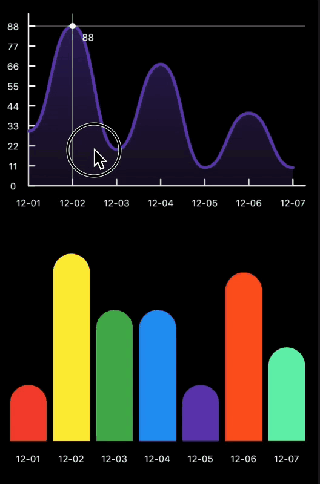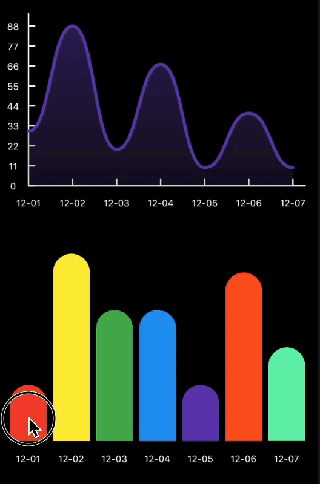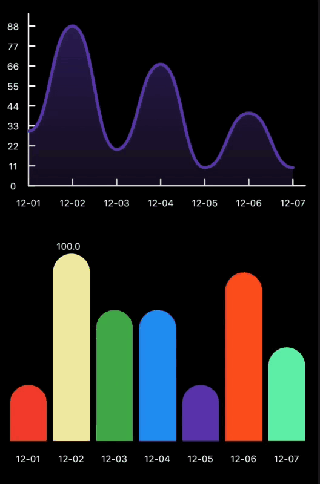
代码已发布到 Dart社区 https://pub.dev/flutter/packages?q=flutter_chart

GitHub仓库链接 https://github.com/good-good-study/flutter_chart

一	二	三	四	五	六	日
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30	31